Az igazságtáblázatok megoldása: 10 lépés

2024 Szerző: John Day | [email protected]. Utoljára módosítva: 2024-01-30 09:40

Az igazságtábla a probléma összes kimenetelének vizualizálásának módja. Ez az utasításkészlet azoknak készült, akik kezdik a diszkrét matematikát. Ma gyakorolni fogunk egy példaproblémát, amely kifejezetten ezekre az utasításokra vonatkozik. Szüksége lesz egy karcoló papírra és egy ceruzára az asztal megjelenítéséhez. Ennek a problémának körülbelül 5 percet kell igénybe vennie azok számára, akik előzetesen ismerik a témát, és körülbelül 10 percet a kezdőknek.

Ebben az utasításkészletben a ~ p Λ q problémára fogunk összpontosítani. Ezzel az igazságtáblázatok értelmezéséhez szükséges szimbólumokat mutatjuk be.

1. lépés: Az igazságtáblázatok megértése

Az igazságtábla egy módja annak, hogy vizualizálja a probléma minden lehetőségét. Az igazságtáblázatok ismerete alapvető szükségesség a diszkrét matematika számára. Itt megtaláljuk a ~ p Λ q egyszerű egyenlet összes eredményét.

2. lépés: A szimbólumok ismerete

Az igazságtábla felé vezető első lépés a jelek megértése. A „~” ebben a konkrét problémában a tagadást jelenti. A „p” és a „q” egyaránt változó. A „Λ” egyenértékű az „és” kifejezéssel. Ezt az egyenletet „nem p és q” -nak kell olvasni, vagyis az egyenlet igaz, ha p nem igaz, és q igaz.

3. lépés: A táblázat formázása

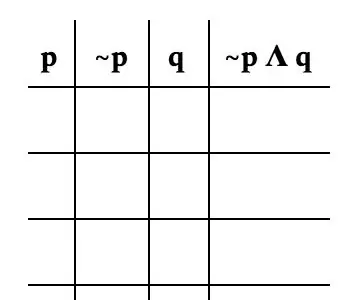
Most a tényleges táblázat kialakítása. Fontos, hogy a problémát minden változó szerint felbontjuk. Ehhez a problémához a következőképpen bontjuk fel: p, ~ p, q és ~ p Λ q. A kép jó példa arra, hogyan kell kinéznie az asztalának.

4. lépés: Igaz és hamis hozzárendelés

Mivel csak két változó létezik, változónként csak négy lehetőség lesz. P esetén felosztjuk a T szóközök felével (igaz), másik felével F -el (hamis).

5. lépés: tagadás

~ P esetén az ellenkező jelet írja, mint p, mivel ~ p ellentéte a p -nek.

6. lépés: "q" változó

Q esetén váltakozhat T és F között, hogy megkapja az összes lehetséges kombinációt. Mivel az egyenlet csak a ~ p -re összpontosít, figyelmen kívül hagyhatjuk a p oszlopot az egyenlet igazságának meghatározásakor. A „Λ” szimbólum azt jelenti, hogy a ~ p és q értéknek is igaznak kell lennie ahhoz, hogy az egyenlet igaz legyen.

7. lépés: Hamis megoldás az utolsó oszlopban

Az első sorban, mivel ~ p F és q T, ~ p Λ q F abban az esetben, ha ~ p F és q T. T.

8. lépés: Az igazság megtalálása az utolsó oszlopban

Ez azt jelenti, hogy az egyetlen T sor a harmadik.

9. lépés: A táblázat befejezése

Ellenőrizze kétszer, hogy a táblázat helyesen van -e megadva. Ezt úgy teheti meg, hogy ellenőrzi a jelek helyességét, és meggyőződik arról, hogy az utolsó oszlop helyesen van -e megadva. Az utolsó oszlop a változók összes lehetséges permutációjának eredménye.

10. lépés: Kész

Most, hogy tudod, hogyan kell elkészíteni egy alapvető igazságtáblázatot, gyakorold tovább! Minél többet gyakorolsz, annál jobban fogod csinálni.