Egyszerű automatikus kondenzátor tesztelő / kapacitásmérő Arduino -val és kézzel: 4 lépés

2024 Szerző: John Day | [email protected]. Utoljára módosítva: 2024-01-30 09:41

Helló!

Ehhez a fizikai egységhez szüksége van:

* 0-12V-os tápegység

* egy vagy több kondenzátor

* egy vagy több töltőellenállás

* stopper

* multiméter a feszültség mérésére

* egy arduino nano

* 16x2 I²C kijelző

* 1 / 4W ellenállások 220, 10k, 4,7M és 1Gohms 1 gohms ellenállással

* dupont huzal

1. lépés: Általános információk a kondenzátorokról

A kondenzátorok nagyon fontos szerepet játszanak az elektronikában. A töltések tárolására szolgálnak, mint szűrő, integrátor stb. De matematikailag sok a kondenzátor. Tehát gyakorolhat exponenciális függvényeket kondenzátorokkal és ezekkel. dolgozz ki. Ha egy kezdetben töltetlen kondenzátort egy ellenálláson keresztül egy feszültségforráshoz csatlakoztatnak, akkor a töltések folyamatosan áramlanak a kondenzátorhoz. A Q töltés növekedésével a Q = C * U képlet szerint (C = a kondenzátor kapacitása) az U feszültség is növekszik a kondenzátoron. A töltőáram azonban egyre inkább csökken, mivel a gyorsan feltöltött kondenzátort egyre nehezebb töltéssel feltölteni. A kondenzátor U (t) feszültsége a következő képletnek felel meg:

U (t) = U0 * (1 exp (-k * t))

U0 a tápegység feszültsége, t az idő és k a töltési folyamat sebességének mértéke. Milyen mérettől függ a k? Minél nagyobb a tárolókapacitás (azaz a kondenzátor C kapacitása), annál lassabban töltődik fel töltésekkel, és annál lassabban nő a feszültség. Minél nagyobb a C, annál kisebb a k. A kondenzátor és a tápegység közötti ellenállás szintén korlátozza a töltés szállítását. Egy nagyobb R ellenállás kisebb I áramot okoz, és ezért másodpercenként kevesebb töltés áramlik a kondenzátorba. Minél nagyobb az R, annál kisebb a k. A helyes kapcsolat k és R vagy C között:

k = 1 / (R * C).

A kondenzátor U (t) feszültsége tehát az U (t) = U0 * (1-exp (-t / (R * C))) képlet szerint növekszik

2. lépés: A mérések

A tanulók a t időpontban írják be az U feszültséget egy táblázatba, majd rajzolják meg az exponenciális függvényt. Ha a feszültség túl gyorsan növekszik, növelnie kell az R ellenállást. A másik oldalon, ha a feszültség túl lassan változik, csökkentse az R értéket.

Ha valaki ismeri az U0 -t, az R ellenállást és az U (t) feszültséget egy bizonyos t idő elteltével, akkor ebből kiszámítható a kondenzátor C kapacitása. Ehhez logaritmizálni kell az egyenletet, és néhány átalakítás után a következőket kapjuk: C = -t / (R * ln (1 - U (t) / U0))

Példa: U0 = 10V, R = 100 kohm, t = 7 másodperc, U (7 mp) = 3,54V. Ekkor C C = 160 μF értéket eredményez.

De van egy második, egyszerű módszer a C kapacitás meghatározására. Nevezetesen, az U (t) feszültség t = R * C után pontosan az U0 63,2% -a.

U (t) = U0 * (1 exp (-R * C / (R * C)) = U0 * (1-exp (-1)) = U0 * 0,632

Mit is jelent ez? A tanulóknak meg kell határozniuk azt az t időt, amely után az U (t) feszültség pontosan az U0 63,2% -a. Konkrétan a fenti példában azt az időt keresik, amely után a kondenzátor feszültsége 10V * 0,632 = 6,3V. Ez a helyzet 16 másodperc után. Ezt az értéket most beillesztjük a t = R * C: 16 = 100000 * C egyenletbe. Ez az eredményt adja: C = 160 μF.

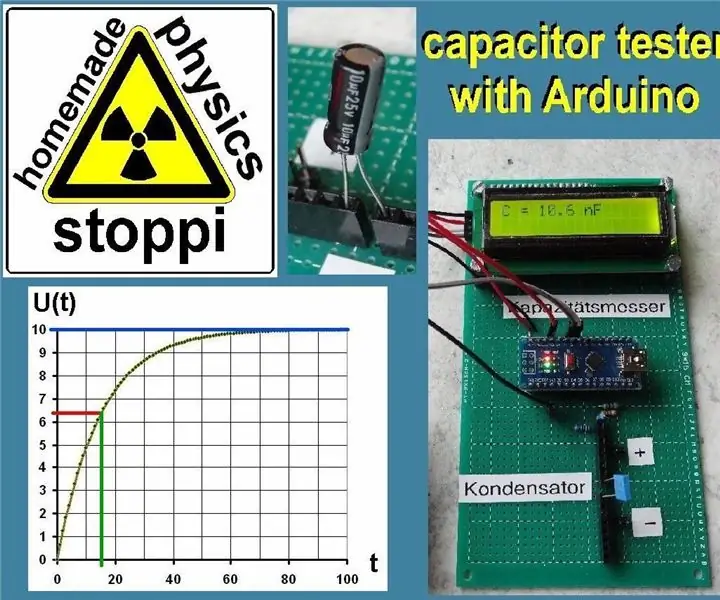
3. lépés: Az Arduino

A gyakorlat végén a kapacitás Arduino segítségével is meghatározható. Ez pontosan kiszámítja a C kapacitást a korábbi módszer szerint. A kondenzátort egy ismert R ellenálláson keresztül 5V -val tölti fel, és meghatározza azt az időt, amely után a kondenzátor feszültsége = 5V * 0,632 = 3,16V. Az Arduino digitális-analóg átalakító esetében az 5V egyenlő 1023. Ezért csak meg kell várnia, amíg az analóg bemenet értéke 1023 * 3,16 / 5 = 647. Ezzel az idővel a C kapacitás kiszámítható. Annak érdekében, hogy a különböző kapacitású kondenzátorok mérhetők legyenek, 3 különböző töltőellenállást használnak. Először egy alacsony ellenállást használnak a töltési idő meghatározására 647 -ig. Ha ez túl rövid, azaz ha a kondenzátor kapacitása túl kicsi, akkor a következő nagyobb töltési ellenállás kerül kiválasztásra. Ha ez is túl kicsi, akkor a mérés végén 1 Gohms ellenállás következik. Ezután a C értéke megjelenik a kijelzőn a megfelelő egységgel (µF, nF vagy pF).

4. lépés: Következtetések

Mit tanulnak a diákok ebben az egységben? Megismerheti a kondenzátorokat, a C kapacitást, az exponenciális függvényeket, a logaritmust, a százalékos számításokat és az Arduino -t. Sokat gondolkodom.

Ez az egység 16-17 éves diákok számára alkalmas. Biztosan átment már az exponenciális függvényen és a matematika logaritmusán. Jó szórakozást az osztályban és az Eurekában!

Nagyon örülnék, ha rám szavazna az osztálytermi természettudományos versenyen. Köszönöm szépen ezt!

Ha érdekel más fizikai projektem, itt a youtube csatornám:

további fizikai projektek: