
Tartalomjegyzék:
- Szerző John Day day@howwhatproduce.com.
- Public 2024-01-30 09:45.
- Utoljára módosítva 2025-01-23 14:48.
Bevezetés
Ez az útmutató azoknak szól, akik érdeklődnek a gyorsulásmérők és giroszkópok, valamint a kombinált IMU -eszközök (inerciális mérőegység) használata iránt elektronikai projektjeikben.
Lefedjük:
- Mit mér a gyorsulásmérő?
- Mit mér a giroszkóp (más néven giroszkóp)?
- Az analóg-digitális (ADC) leolvasások átalakítása ezekből az érzékelőkből fizikai egységekbe (ezek a következők: g gyorsulásmérő, deg/s giroszkóp esetén)
- Hogyan lehet kombinálni a gyorsulásmérő és a giroszkóp leolvasásait annak érdekében, hogy pontos információkat kapjunk a készülék dőlésszögéről az alaplaphoz képest
A cikk során megpróbálom a minimálisra csökkenteni a matematikát. Ha tudja, mi a Sine/Cosinus/Tangent, akkor képesnek kell lennie arra, hogy megértse és felhasználhassa ezeket az ötleteket a projektjében, függetlenül attól, hogy milyen platformot használ: Arduino, Propeller, Basic Stamp, Atmel chipek, Microchip PIC stb.
Vannak emberek, akik úgy vélik, hogy komplex matematikára van szüksége az IMU egység használatához (komplex FIR vagy IIR szűrők, például Kalman szűrők, Parks-McClellan szűrők stb.). Mindezeket kutathatja, és csodálatos, de összetett eredményeket érhet el. A dolgok magyarázásának módja csak alapvető matematikát igényel. Nagy híve vagyok az egyszerűségnek. Úgy gondolom, hogy az egyszerű rendszert könnyebb ellenőrizni és felügyelni, emellett sok beágyazott eszköz nem rendelkezik erővel és erőforrásokkal ahhoz, hogy mátrixszámításokat igénylő összetett algoritmusokat hajtson végre.
Példaként egy új IMU egységet, az Acc_Gyro Accelerometer + Gyro IMU -t hozok fel. Ennek az eszköznek a paramétereit fogjuk használni az alábbi példákban. Ez az egység jó eszköz a kezdéshez, mivel 2 eszközből áll:
- LIS331AL (adatlap) - háromtengelyes 2G gyorsulásmérő - LPR550AL (adatlap) - kéttengelyes dőlésszög, 500 fok/sec giroszkóp
Együtt képviselik az 5 fokos szabadság inerciális mérési egységet. Ez most egy fantasztikus név! Ennek ellenére a fantázianév mögött egy nagyon hasznos kombinációs eszköz található, amelyet ebben az útmutatóban részletesen ismertetünk.
Lépés: A gyorsulásmérő
Ennek az egységnek a megértéséhez kezdjük a gyorsulásmérővel. Amikor a gyorsulásmérőkre gondolunk, gyakran hasznos olyan kockát ábrázoló dobozt ábrázolni, amelyben golyó van. Elképzelhet mást, mint egy sütit vagy egy fánkot, de én egy golyót:
Ha ezt a dobozt olyan helyre vesszük, ahol nincsenek gravitációs mezők, vagy ha nincs más mező, amely befolyásolhatja a labda helyzetét - a labda egyszerűen lebeg a doboz közepén. El lehet képzelni, hogy a doboz a világűrben van, messze a kozmikus testektől, vagy ha ilyen helyet nehéz megtalálni, akkor képzeljünk el legalább egy űrhajót, amely a bolygó körül kering, ahol minden súlytalan állapotban van. A fenti képen látható, hogy minden tengelyhez hozzárendelünk egy falfalat (eltávolítottuk az Y+ falat, hogy be tudjunk nézni a dobozba). Képzelje el, hogy minden fal nyomásérzékeny. Ha hirtelen balra mozgatjuk a dobozt (1g = 9,8m/s^2 gyorsulással gyorsítjuk), akkor a labda X- falba ütközik. Ezután megmérjük a labdát a falra kifejtett nyomóerőt, és -1g értéket adunk ki az X tengelyen.
Kérjük, vegye figyelembe, hogy a gyorsulásmérő valóban érzékel egy erőt, amely a gyorsulási vektorral ellentétes irányba van irányítva. Ezt az erőt gyakran inerciális erőnek vagy fiktív erőnek nevezik. Egy dolgot tanuljon meg ebből, hogy a gyorsulásmérő közvetett módon méri a gyorsulást az egyik falára kifejtett erő révén (modellünk szerint ez lehet rugó vagy valami más a valós élet gyorsulásmérőiben). Ezt az erőt a gyorsulás okozhatja, de amint azt a következő példában látni fogjuk, nem mindig a gyorsulás okozza.
Ha magunkhoz vesszük a modellünket és a Földre tesszük, a golyó a Z-falra esik, és 1 g erőt gyakorol az alsó falra, amint az az alábbi képen látható:
Ebben az esetben a doboz nem mozog, de továbbra is -1 g értéket kapunk a Z tengelyen. A labdát a falra gyakorolt nyomást gravitációs erő okozta. Elméletileg ez másfajta erő is lehet - ha például azt képzeli, hogy a labdánk fémes, a mágnes elhelyezése a doboz mellett elmozdíthatja a labdát, így az egy másik falnak ütközik. Ezt csak azért mondták, hogy bebizonyítsák, hogy lényegében a gyorsulásmérő nem gyorsul, hanem erő. Előfordul, hogy a gyorsulás inerciális erőt okoz, amelyet a gyorsulásmérő erőérzékelő mechanizmusa rögzít.
Bár ez a modell nem pontosan a MEMS érzékelő felépítésének módja, gyakran hasznos a gyorsulásmérővel kapcsolatos problémák megoldásában. Valójában vannak hasonló érzékelők, amelyekben fém golyók vannak, ezeket tilt kapcsolóknak nevezik, azonban primitívebbek, és általában csak azt tudják megmondani, hogy az eszköz bizonyos tartományban dől -e vagy sem, nem pedig a dőlés mértékét.
Eddig egyetlen tengelyen elemeztük a gyorsulásmérő kimenetét, és ez minden, amit egyetlen tengelyes gyorsulásmérővel kaphat. A triaxiális gyorsulásmérők valódi értéke onnan származik, hogy mindhárom tengelyen képesek érzékelni a tehetetlenségi erőket. Térjünk vissza a dobozmodellhez, és forgassuk el a dobozt 45 fokkal jobbra. A labda most két falat fog érinteni: Z- és X-, amint az alábbi képen látható:
A 0,71 értékek nem tetszőlegesek, valójában az SQRT (1/2) közelítése. Ez világosabb lesz, amint bemutatjuk a gyorsulásmérő következő modelljét.
Az előző modellben rögzítettük a gravitációs erőt, és elforgattuk képzeletbeli dobozunkat. Az utolsó 2 példában a kimenetet két különböző dobozpozícióban elemeztük, míg az erővektor állandó maradt. Bár ez hasznos volt annak megértésében, hogy a gyorsulásmérő hogyan hat kölcsönhatásba a külső erőkkel, célszerűbb számításokat végezni, ha rögzítjük a koordináta -rendszert a gyorsulásmérő tengelyeire, és elképzeljük, hogy az erővektor körülöttünk forog.
Kérjük, nézze meg a fenti modellt, megőriztem a tengelyek színeit, hogy mentálisan át tudjon lépni az előző modellről az újra. Képzeljük csak el, hogy az új modell minden tengelye merőleges az előző modell dobozának megfelelő oldalára. Az R vektor az erővektor, amelyet a gyorsulásmérő mér (ez lehet a gravitációs erő vagy a tehetetlenségi erő a fenti példákból, vagy a kettő kombinációja). Rx, Ry, Rz az R vektor vetülete az X, Y, Z tengelyekre. Kérjük, vegye figyelembe a következő összefüggést:
R^2 = Rx^2 + Ry^2 + Rz^2 (1. egyenlet)
ami alapvetően a Pitagorasz -tétel megfelelője 3D -ben.
Ne feledje, hogy egy kicsit korábban elmondtam, hogy az SQRT (1/2) ~ 0,71 értékei nem véletlenszerűek. Ha csatlakoztatja őket a fenti képlethez, emlékeztetve arra, hogy a gravitációs erőnk 1 g volt, ellenőrizhetjük, hogy:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
egyszerűen R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) helyettesítésével az 1. egyenletben
Az elmélet hosszú preambuluma után egyre közelebb kerülünk a gyorsulásmérőkhöz. Az Rx, Ry, Rz értékek lineárisan kapcsolódnak azokhoz az értékekhez, amelyeket a valós élet gyorsulásmérője ad ki, és amelyeket különböző számítások elvégzésére használhat.
Mielőtt odaérnénk, beszéljünk egy kicsit arról, hogy a gyorsulásmérők hogyan továbbítják ezt az információt nekünk. A legtöbb gyorsulásmérő két kategóriába sorolható: digitális és analóg. A digitális gyorsulásmérők soros protokoll, például I2C, SPI vagy USART használatával nyújtanak információt, míg az analóg gyorsulásmérők egy előre meghatározott tartományon belüli feszültségszintet adnak ki, amelyet egy ADC (analóg -digitális átalakító) modul segítségével kell digitális értékre konvertálni. Nem részletezem részletesen az ADC működését, részben azért, mert ilyen kiterjedt téma, részben pedig azért, mert platformonként eltérő. Egyes mikrovezérlők beépített ADC modulokkal rendelkeznek, némelyiküknek külső komponensekre lesz szükségük az ADC konverziók végrehajtásához. Függetlenül attól, hogy milyen típusú ADC modult használ, egy adott tartományba eső értéket kap. Például egy 10 bites ADC modul 0..1023 tartományban ad ki értéket, vegye figyelembe, hogy 1023 = 2^10 -1. A 12 bites ADC modul a 0..4095 tartományba eső értéket ad ki, vegye figyelembe, hogy 4095 = 2^12-1.
Folytassuk egy egyszerű példa figyelembevételével, tegyük fel, hogy a 10 bites ADC modul a következő értékeket adta meg nekünk a három gyorsulásmérő csatornához (tengelyhez):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Minden ADC modulnak lesz referencia feszültsége, tegyük fel, hogy példánkban 3,3 V. A 10 bites adc érték feszültséggé alakításához a következő képletet használjuk:
VoltsRx = AdcRx * Vref / 1023
Egy gyors megjegyzés itt: hogy a 8 bites ADC esetén az utolsó osztó 255 = 2 ^ 8 -1, a 12 bites ADC esetén az utolsó osztó 4095 = 2 ^ 12 -1.
Ezt a képletet mindhárom csatornára alkalmazva kapjuk:
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (az összes eredményt 2 tizedesjegyre kerekítjük) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V volt
Minden gyorsulásmérő nulla g-os feszültséggel rendelkezik, specifikációban megtalálható, ez az a feszültség, amely 0 g-nak felel meg. Ahhoz, hogy előjeles feszültségértéket kapjunk, ki kell számolnunk az eltolást erről a szintről. Tegyük fel, hogy a 0g feszültségszintünk VzeroG = 1,65V. A feszültségeltolódásokat a nulla g feszültségről a következőképpen számítjuk ki:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
A gyorsulásmérőnk leolvasása voltban volt, még mindig nem g -ban (9,8 m/s^2), a végső konverzióhoz a gyorsulásmérő érzékenységét alkalmazzuk, általában mV/g -ban. Tegyük fel, hogy az érzékenységünk = 478,5 mV/g = 0,4785V/g. Az érzékenységi értékek a gyorsulásmérő specifikációiban találhatók. A g -ban kifejezett végső erőértékek kiszámításához a következő képletet használjuk:
Rx = DeltaVoltsRx / Érzékenység
Rx = 0.24V / 0.4785V / g = ~ 0.5g Ry = 0.38V / 0.4785V / g = ~ 0.79g Rz = 0.16V / 0.4785V / g = ~ 0.33g
Természetesen minden lépést egy képletben egyesíthetnénk, de végigmentem az összes lépésen, hogy világossá tegyük, hogyan juthat el az ADC -leolvasásokból a g -ban kifejezett erővektor -összetevőbe.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Érzékenység (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Érzékenység Rz = (AdcRz * Vref / 1023 - VzeroG) / Érzékenység
Most már mindhárom komponensünk megvan, amelyek meghatározzák a tehetetlenségi erővektorunkat, ha az eszköz nincs kitéve más erőknek, mint a gravitáció, akkor feltételezhetjük, hogy ez a gravitációs erővektorunk iránya. Ha ki akarja számítani az eszköz dőlésszögét a talajhoz képest, kiszámíthatja a vektor és a Z tengely közötti szöget. Ha Önt is érdekli a tengelyenkénti dőlésirány, akkor ezt az eredményt két részre oszthatja: az X és Y tengely dőlése, amely a gravitációs vektor és az X / Y tengely közötti szögként számítható. Ezeknek a szögeknek a kiszámítása egyszerűbb, mint gondolná, most, hogy kiszámítottuk az Rx, Ry és Rz értékeket. Térjünk vissza az utolsó gyorsulásmérő modellünkhöz, és tegyünk néhány további megjegyzést:
Az általunk érdekelt szögek az X, Y, Z tengelyek és az R erővektor közötti szögek. Ezeket a szögeket Axr, Ayr, Azr. Az R és Rx által alkotott derékszögű háromszögből észreveheti, hogy:
cos (Axr) = Rx / R, és hasonlóan: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Az Eq.1 -ből levonhatjuk, hogy R = SQRT (Rx^2 + Ry^2 + Rz^2).
Most meg tudjuk találni a szögeinket az arccos () függvény (az inverz cos () függvény) használatával:
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
Hosszú utat tettünk meg a gyorsulásmérő modelljének megmagyarázásáért, csak hogy ezekhez a képletekhez jussunk. Alkalmazásaitól függően érdemes lehet bármilyen köztes képleteket használni. Hamarosan bemutatjuk a giroszkóp modellt is, és meglátjuk, hogyan lehet a gyorsulásmérő és a giroszkóp adatait kombinálni, hogy még pontosabb dőlésbecsléseket lehessen biztosítani.
Mielőtt azonban ezt megtennénk, tegyünk néhány hasznos megjegyzést:
cosX = cos (Axr) = Rx / R hangulatos = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Ezt a triplettet gyakran Direction Cosinus -nak hívják, és alapvetően azt az egységvektorot (1 hosszúságú vektor) ábrázolja, amelynek iránya megegyezik az R vektorunkéval. Könnyen ellenőrizheti, hogy:
SQRT (cosX^2 + hangulatos^2 + cosZ^2) = 1
Ez egy szép tulajdonság, mivel mentesít minket az R vektor modulusának (hosszának) figyelésétől. Gyakran előfordul, hogy ha csak a tehetetlenségi vektor irányába vagyunk kíváncsiak, akkor érdemes normalizálni a modulusát, hogy egyszerűsítsük más számításokat.
2. lépés: Giroszkóp
Nem fogunk bevezetni semmilyen egyenértékű dobozmodellt a giroszkóphoz, mint a gyorsulásmérő esetében, hanem egyenesen a második gyorsulásmérő modellhez ugrunk, és megmutatjuk, mit mér a giroszkóp e modell szerint.
Minden giroszkópcsatorna méri az egyik tengely körüli forgást. Például egy kéttengelyes giroszkóp mérni fogja az X és Y tengely körüli (vagy egyesek "kb.") Forgást. Hogy ezt a forgást számokkal fejezzük ki, tegyünk néhány jelölést. Először határozzuk meg:
Rxz - az R tehetetlenségi erővektor vetülete az XZ síkra Ryz - az R tehetetlenségi erővektor vetülete az YZ síkra
Az Rxz és Rz által alkotott derékszögű háromszögből Pitagorasz-tételt használva kapjuk:
Rxz^2 = Rx^2 + Rz^2, és hasonlóképpen: Ryz^2 = Ry^2 + Rz^2
vegye figyelembe azt is, hogy:
R^2 = Rxz^2 + Ry^2, ez az Eq.1 és a fenti egyenletekből származtatható, vagy az R és Ryz által alkotott derékszögű háromszögből R^2 = Ryz^2 + Rx^2
Ebben a cikkben nem fogjuk használni ezeket a képleteket, de hasznos megjegyezni a modellünk összes értéke közötti kapcsolatot.
Ehelyett a Z tengely és az Rxz, Ryz vektorok közötti szöget határozzuk meg a következőképpen:
Axz - az Rxz (R vetülete az XZ síkon) és az Ayz Z tengely közötti szög - a Ryz (R vetülete YZ síkon) és Z tengely közötti szög
Most közelebb kerülünk ahhoz, amit a giroszkóp mér. A giroszkóp méri a fent meghatározott szögek változásának sebességét. Más szavakkal, olyan értéket ad ki, amely lineárisan kapcsolódik ezen szögek változási sebességéhez. Ennek magyarázataként tegyük fel, hogy a t0 időpontban megmértük az Y tengely körüli forgásszöget (ez Axz -szög lenne), és Axz0 -ként definiáljuk, majd ezt a szöget egy későbbi t1 időpontban mértük, és ez volt az Axz1. A változás mértékét a következőképpen kell kiszámítani:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Ha az Axz -ot fokokban, az időt pedig másodpercben fejezzük ki, akkor ezt az értéket deg/s -ban fejezzük ki. Ezt méri a giroszkóp.
A gyakorlatban a giroszkóp (kivéve, ha speciális digitális giroszkópról van szó) ritkán ad meg deg/s -ban kifejezett értéket. A gyorsulásmérőhöz hasonlóan kap egy ADC értéket, amelyet deg/s -ra kell konvertálnia az Eq -hez hasonló képlet segítségével. 2, amit a gyorsulásmérőhöz definiáltunk. Bemutatjuk az ADC -t a giroszkóp deg/s konverziós képletéhez (feltételezzük, hogy 10 bites ADC modult használunk, 8 bites ADC esetén cserélje ki az 1023 -at 255 -tel, a 12 bites ADC -t cserélje ki az 1023 -at 4095 -tel).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Érzékenység Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Érzékenység
Az AdcGyroXZ, AdcGyroYZ - az adc modulunkból származnak, és azokat a csatornákat jelölik, amelyek az R vektor vetületének forgását XZ -ben YZ síkokban mérik, ami megegyezik azzal, hogy a forgás Y és X tengely körül történt.
Vref - ez az ADC referenciafeszültség, amelyet a 3.3 V -nál fogunk használni a VzeroRate alatti példában - a nulla sebességű feszültség, más szóval az a feszültség, amelyet a giroszkóp akkor ad ki, ha nem forog, az Acc_Gyro kártya esetében például 1,23 V (ezeket az értékeket a specifikációkban találja) Érzékenység - a giroszkóp érzékenysége mV / (deg / s) -ban kifejezve, gyakran mV / deg / s -ként írva, alapvetően megmondja, hogy hány mV lesz a giroszkóp kimenete nő, ha a fordulatszámot egy fokkal/másodperccel növeli. Az Acc_Gyro kártya érzékenysége például 2 mV/deg/s vagy 0,002 V/deg/s
Vegyünk egy példát, tegyük fel, hogy ADC modulunk a következő értékeket adta vissza:
AdcGyroXZ = 571 AdcGyroXZ = 323
A fenti képlet és az Acc_Gyro tábla specifikációs paraméterei segítségével a következőket kapjuk:
RateAxz = (571 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ 306 deg/s RateAyz = (323 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ -94 fok/s
Más szóval a készülék az Y tengely körül (vagy mondhatjuk, hogy XZ síkban forog) 306 °/s sebességgel forog, az X tengely körül (vagy mondhatjuk, hogy YZ síkban forog) - 94 fok/s. Kérjük, vegye figyelembe, hogy a negatív előjel azt jelenti, hogy a készülék a hagyományos pozitív irányba ellentétesen forog. Megállapodás szerint az egyik forgásirány pozitív. Egy jó giroszkóp specifikációs lap megmutatja, hogy melyik irány pozitív, különben meg kell találnia, ha kísérletezik az eszközzel, és megjegyzi, hogy melyik forgásirány növeli a feszültséget a kimeneti tüskén. Ezt legjobban oszcilloszkóppal lehet megtenni, mivel amint megállítja a forgást, a feszültség visszaesik a nulla sebességű szintre. Ha multimétert használ, akkor legalább néhány másodpercig állandó forgási sebességet kell tartania, és meg kell jegyeznie a feszültséget a forgás során, majd hasonlítsa össze a nulla sebességű feszültséggel. Ha nagyobb, mint a nulla sebességű feszültség, az azt jelenti, hogy a forgásirány pozitív.
3. lépés: A gyorsulásmérő és a giroszkóp kombinálása
Az összes összekapcsolása - A gyorsulásmérő és a giroszkóp adatainak kombinálása
Ha ezt a cikket olvassa, valószínűleg beszerezte vagy tervezi beszerezni az IMU -eszközt, vagy valószínűleg azt tervezi, hogy külön gyorsulásmérőből és giroszkópból készül.
A gyorsulásmérőt és a giroszkópot kombináló kombinált IMU -eszköz használatának első lépése a koordináta -rendszerek összehangolása. Ennek legegyszerűbb módja, ha a gyorsulásmérő koordináta -rendszerét választja referencia -koordináta -rendszerként. A legtöbb gyorsulásmérő adatlapja megjeleníti az X, Y, Z tengelyek irányát a fizikai chip vagy eszköz képéhez képest. Például itt vannak az X, Y, Z tengelyek irányai, amint az az Acc_Gyro kártya specifikációiban látható:
A következő lépések a következők:
Azonosítsa a giroszkóp kimeneteit, amelyek megfelelnek a fent tárgyalt RateAxz, RateAyz értékeknek. Határozza meg, hogy ezeket a kimeneteket meg kell -e fordítani a giroszkóp gyorsulásmérőhöz viszonyított fizikai helyzete miatt
Ne feltételezze, hogy ha a giroszkóp kimenete X vagy Y jelzésű, akkor az a gyorsulásmérő koordináta -rendszer bármely tengelyének megfelel, még akkor is, ha ez a kimenet egy IMU egység része. A legjobb módszer a tesztelés. Feltételezve, hogy rögzítette a giroszkóp helyzetét a gyorsulásmérőhöz képest. Feltételezzük, hogy a giroszkóp és a gyorsulásmérő szegélye párhuzamos egymással, azaz a gyro -t 90 fokos szögben helyezi el a gyorsulásmérő chiphez képest. Ha beszerzett egy IMU -táblát, nagy valószínűséggel már így is igazodik. Ebben a cikkben nem tárgyaljuk azokat a modelleket, ahol a giroszkóp szabálytalan szögben van elhelyezve a gyorsulásmérőhöz képest (mondjuk 45 vagy 30 fok), bár ez bizonyos alkalmazásokban hasznos lehet.
Íme egy mintasorozat annak meghatározására, hogy a giroszkóp melyik kimenete megfelel a fent tárgyalt RateAxz értéknek.
- kezdje a készülék vízszintes helyzetbe helyezésével. A gyorsulásmérő X és Y kimenetei is nulla g feszültséget adnak ki (például az Acc_Gyro kártya esetén ez 1,65 V)
- Ezután kezdje el forgatni a készüléket az Y tengely körül, egy másik módja annak, hogy az eszközt XZ síkban forgassa el, így az X és Z gyorsulásmérő kimenete megváltozik, és az Y kimenet állandó marad. - miközben a készüléket állandó sebességgel forgatja, és a giroszkóp kimenete megváltozik, a többi giroszkóp kimenetnek állandónak kell maradnia - az Y tengely körüli forgás során megváltozott giroszkóp kimenet (XZ síkban történő elforgatás) megadja az AdcGyroXZ bemeneti értékét, kiszámítjuk a RateAxz értéket - az utolsó lépés annak biztosítása, hogy a forgásirány megfeleljen modellünknek, bizonyos esetekben előfordulhat, hogy meg kell fordítania a RateAxz értékét a giroszkóp gyorsulásmérőhöz viszonyított fizikai helyzete miatt - hajtsa végre újra a fenti tesztet, forgassa el a készüléket az Y tengely, ezúttal figyelje a gyorsulásmérő X kimenetét (modellünkben AdcRx). Ha az AdcRx nő (az első 90 fokos elforgatás vízszintes helyzetből), akkor az AdcGyroXZ -nek is növekednie kell. Ellenkező esetben meg kell fordítania a RateAxz -ot, ezt úgy érheti el, hogy előjelet ad az Eq.3 -ba, az alábbiak szerint:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Érzékenység, ahol az InvertAxz értéke 1 vagy -1
Ugyanezt a teszt vesszőt lehet elvégezni a RateAyz esetében is, az eszköz X tengelye körüli elforgatásával, és azonosíthatja, hogy melyik giroszkóp kimenet felel meg a RateAyz -nek, és ha meg kell fordítani. Miután megkapta az InvertAyz értékét, a következő képletet kell használnia a RateAyz kiszámításához:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Érzékenység
Ha ezeket a teszteket elvégezné az Acc_Gyro táblán, a következő eredményeket kapná:
- a RateAxz kimeneti csapja GX4 és InvertAxz = -1. - a RateAyz kimeneti csapja GY4 és InvertAyz = -1
Innentől kezdve úgy tekintjük, hogy az IMU -t úgy állította be, hogy ki tudja számítani a helyes értékeket az Axr, Ayr, Azr (1. rész szerinti gyorsulásmérő) és RateAxz, RateAyz értékekhez (a 2. részben meghatározottak szerint).). Ezután elemezzük ezen értékek közötti összefüggéseket, amelyek hasznosnak bizonyulnak ahhoz, hogy pontosabb becslést kapjunk az eszköz dőlésszögéről az alap síkhoz képest.
Lehet, hogy már most felteszi magának a kérdést, hogy ha a gyorsulásmérő modellje már megadta az Axr, Ayr, Azr dőlésszögeit, miért akarunk a giroszkóp adataival bajlódni? A válasz egyszerű: a gyorsulásmérő adatait nem lehet mindig 100%-ban megbízni. Több oka is van, ne feledje, hogy a gyorsulásmérő a tehetetlenségi erőt méri, az ilyen erőt a gravitáció (és ideális esetben csak a gravitáció) okozhatja, de az eszköz gyorsulása (mozgása) is okozhatja. Ennek eredményeként még akkor is, ha a gyorsulásmérő viszonylag stabil állapotban van, még mindig nagyon érzékeny a rezgésre és általában a mechanikai zajra. Ez a fő oka annak, hogy a legtöbb IMU rendszer giroszkópot használ a gyorsulásmérő hibáinak kiegyenlítésére. De hogyan történik ez? És a giroszkóp zajmentes?
A giroszkóp azonban nem mentes a zajtól, mivel a forgást méri, kevésbé érzékeny a lineáris mechanikai mozgásokra, a gyorsulásmérő által elszenvedett zajra, azonban a giroszkópnak más típusú problémái is vannak, például a sodródás (nem tér vissza a nulla értékhez) amikor a forgás leáll). Mindazonáltal a gyorsulásmérőből és a giroszkópból származó adatok átlagolásával viszonylag jobb becslést kaphatunk a készülék aktuális dőlésszögéről, mint amit önmagában a gyorsulásmérő adatainak felhasználásával kapnánk.
A következő lépésekben bemutatok egy algoritmust, amelyet a Kálmán -szűrőben használt ötletek inspiráltak, de ez sokkal egyszerűbb és könnyebben megvalósítható beágyazott eszközökön. Előtte nézzük meg, hogy mit szeretnénk kiszámítani az algoritmusunknak. Nos, a gravitációs erővektor R = [Rx, Ry, Rz] iránya, amelyből más értékeket, például Axr, Ayr, Azr vagy cosX, cosy, cosZ származtathatunk, amelyek képet adnak eszközünk dőlésszögéről az alap síkhoz viszonyítva az 1. részben tárgyaljuk ezen értékek közötti kapcsolatot. Mondhatnánk - nem rendelkezünk -e már ezekkel az Rx, Ry, Rz értékekkel az 1. rész 2. egyenletéből? Nos, igen, de ne feledje, hogy ezek az értékek csak a gyorsulásmérő adataiból származnak, így ha közvetlenül az alkalmazásban szeretné használni őket, akkor nagyobb zajt kaphat, mint amennyit az alkalmazása elvisel. A további zavarok elkerülése érdekében határozzuk meg újra a gyorsulásmérő méréseit az alábbiak szerint:
Racc - a gyorsulásmérővel mért tehetetlenségi erővektor, amely a következő komponensekből áll (X, Y, Z tengelyre vetített vetületek):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Érzékenység RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Érzékenység RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Érzékenység
Eddig rendelkezünk olyan mért értékekkel, amelyeket tisztán a gyorsulásmérő ADC értékeiből kaphatunk. Ezt az adathalmazt "vektornak" nevezzük, és a következő jelölést fogjuk használni.
Racc = [RxAcc, RyAcc, RzAcc]
Mivel a Racc ezen összetevői a gyorsulásmérő adataiból nyerhetők, úgy tekinthetjük az algoritmusunk bemenetének.
Kérjük, vegye figyelembe, hogy mivel a Racc a gravitációs erőt méri, akkor igaza lesz, ha feltételezi, hogy ennek a vektornak az alábbiakban meghatározott hossza egyenlő vagy közel 1 g.
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2), Azonban annak biztosítása érdekében érdemes ezt a vektort az alábbiak szerint frissíteni:
Racc (normalizált) = [RxAcc/| Racc |, RyAcc/| Racc |, RzAcc/| Racc |].
Ez biztosítja, hogy a normalizált Racc vektor hossza mindig 1 legyen.
Ezután új vektort mutatunk be, és hívjuk
Pihenés = [RxEst, RyEst, RzEst]
Ez lesz az algoritmusunk kimenete, ezek a giroszkóp adatai és a korábbi becsült adatok alapján korrigált értékek.
Az algoritmusunk ezt fogja tenni: - a gyorsulásmérő azt mondja nekünk: "Ön most Racc pozícióban van" - azt mondjuk: "Köszönöm, de hadd nézzem meg" kiadunk egy új becsült vektor Rest. - a pihenést a "legjobb megoldásunknak" tekintjük a készülék jelenlegi helyzetét illetően.
Lássuk, hogyan tudjuk működésbe hozni.
A sorozatot azzal kezdjük, hogy megbízunk a gyorsulásmérőnkben, és hozzárendeljük:
Pihenés (0) = Racc (0)
Egyébként ne feledje, hogy a Rest és a Racc vektorok, így a fenti egyenlet csak egy egyszerű módja annak, hogy három egyenletkészletet írjon, és kerülje az ismétlést:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Ezután rendszeres méréseket végezünk T másodperc azonos időközönként, és új méréseket kapunk, amelyeket Racc (1), Racc (2), Racc (3) és így tovább definiálunk. Új becsléseket is kiadunk minden egyes időközönként Pihenés (1), Pihenés (2), Pihenés (3) és így tovább.
Tegyük fel, hogy az n lépésnél tartunk. Két ismert értékkészletünk van, amelyeket használni szeretnénk:
Pihenés (n -1) - korábbi becslésünk, pihenéssel (0) = Racc (0) Racc (n) - jelenlegi gyorsulásmérő mérésünk
Mielőtt kiszámíthatnánk a pihenőidőt (n), vezessünk be egy új mért értéket, amelyet a giroszkópunkból és egy korábbi becslésből kaphatunk.
Rgyro -nak hívjuk, és ez is egy vektor, amely 3 komponensből áll:
Rgyro = [RxGyro, RyGyro, RzGyro]
Ezt a vektort egyenként fogjuk kiszámítani. Kezdjük az RxGyro -val.
Kezdjük azzal, hogy megfigyeljük a giroszkóp modellünkben a következő összefüggést, az Rz és Rxz által alkotott derékszögű háromszögből azt a következtetést vonhatjuk le:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Az Atan2 olyan funkció lehet, amelyet még soha nem használt, hasonló az atanhoz, kivéve, hogy a (-PI, PI) tartományban ad vissza értékeket, szemben az (-PI/2, PI/2) értékkel, amelyet az atan adott vissza, és ehhez 2 érv egy helyett. Lehetővé teszi számunkra, hogy az Rx, Rz két értékét a 360 fok teljes tartományában (-PI-PI) szögekké alakítsuk át. Az atan2 -ről itt olvashat bővebben.
Tehát az RxEst (n-1) és az RzEst (n-1) ismeretében megtalálhatjuk:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Ne feledje, hogy a giroszkóp az Axz -szög változásának sebességét méri. Tehát az új Axz (n) szöget a következőképpen tudjuk megbecsülni:
Axz (n) = Axz (n-1) + arányAxz (n) * T
Ne feledje, hogy a RateAxz giroszkóp ADC leolvasásainkból szerezhető be. Egy pontosabb képlet az alábbiak szerint kiszámított átlagos forgási sebességet használhatja:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Ugyanígy megtalálhatjuk:
Ayz (n) = Ayz (n-1) + RátAyz (n) * T
Oké, most Axz (n) és Ayz (n) van. Hová megyünk innen az RxGyro/RyGyro levonásához? Eq. Az 1. ábra szerint az Rgyro vektor hosszát a következőképpen írhatjuk fel:
| Rgyro | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
Azért is, mert normalizáltuk a Racc vektorunkat, feltételezhetjük, hogy hossza 1, és nem változott a forgatás után, így viszonylag biztonságosan írható:
| Rgyro | = 1
Vegyünk átmenetileg rövidebb jelölést az alábbi számításokhoz:
x = RxGyro, y = RyGyro, z = RzGyro
A fenti összefüggések segítségével írhatjuk:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
Osszuk el a tört számlálóját és nevezőjét SQRT -vel (x^2 + z^2)
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
Vegye figyelembe, hogy x / SQRT (x^2 + z^2) = sin (Axz), tehát:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Most szorozzuk meg az SQRT -ben lévő tört számlálóját és nevezőjét z^2 -vel
x = sin (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
Vegye figyelembe, hogy z / SQRT (x^2 + z^2) = cos (Axz) és y / z = tan (Ayz), tehát végül:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
Visszatérve a jelölésünkhöz kapjuk:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
ugyanígy találjuk
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
Most végre megtalálhatjuk:
RzGyro = Jel (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
Hol előjel (RzGyro) = 1, ha RzGyro> = 0, és előjel (RzGyro) = -1, ha RzGyro <0.
Ennek becslésének egyik egyszerű módja a következő:
Jel (RzGyro) = Jel (RzEst (n-1))
A gyakorlatban legyen óvatos, ha az RzEst (n-1) közel van a 0-hoz. Ebben az esetben kihagyhatja a giroszkóp fázist, és hozzárendelheti: Rgyro = Pihenés (n-1). Az Rz referenciaként szolgál az Axz és Ayz szögek kiszámításához, és amikor 0 -hoz közelít, az értékek túlfolyhatnak és rossz eredményeket válthatnak ki. A nagy lebegőpontos számok tartományában lesz, ahol a tan () / atan () függvények megvalósításai pontatlanok lehetnek.
Foglaljuk össze tehát az eddigieket, az algoritmus n lépésénél járunk, és kiszámítottuk a következő értékeket:
Racc - Rgyro gyorsulásmérőnk aktuális értékei - nyugalmi (n -1) és aktuális giroszkóp leolvasása
Milyen értékeket használunk a frissített (n) becslés kiszámításához? Valószínűleg sejtette, hogy mindkettőt használni fogjuk. Súlyozott átlagot fogunk használni, hogy:
Pihenés (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Egyszerűsíthetjük ezt a képletet, ha a tört számlálóját és nevezőjét is elosztjuk w1 -gyel.
Pihenés (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
és w2/w1 = wGyro helyettesítése után kapjuk:
Pihenés (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
A fenti fórumban a wGyro elmondja, mennyire bízunk a giroszkópunkban a gyorsulásmérőnkhöz képest. Ez az érték kísérletileg választható, általában az 5..20 közötti értékek jó eredményeket eredményeznek.
Ennek az algoritmusnak a fő különbsége a Kalman szűrőtől az, hogy ez a súly viszonylag rögzített, míg a Kalman szűrőben a súlyok folyamatosan frissülnek a gyorsulásmérő leolvasott zajjai alapján. A Kalman szűrő arra törekszik, hogy "a legjobb" elméleti eredményeket adja, míg ez az algoritmus "elég jó" eredményeket adhat a gyakorlati alkalmazáshoz. Kivitelezhet egy algoritmust, amely a mért zajtényezőktől függően beállítja a wGyro -t, de a rögzített értékek a legtöbb alkalmazásnál jól működnek.
Egy lépésre vagyunk attól, hogy megkapjuk frissített becsült értékeinket:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Most normalizáljuk újra ezt a vektort:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
És készek vagyunk megismételni a körünket.
Ez az útmutató eredetileg a starlino.com webhelyen jelent meg, néhány könnyű szerkesztést végeztem, és engedéllyel újra közzétettem. Köszi Starlino!
Ajánlott:
MPU 6050 giroszkóp, gyorsulásmérő kommunikáció az Arduino -val (Atmega328p): 5 lépés
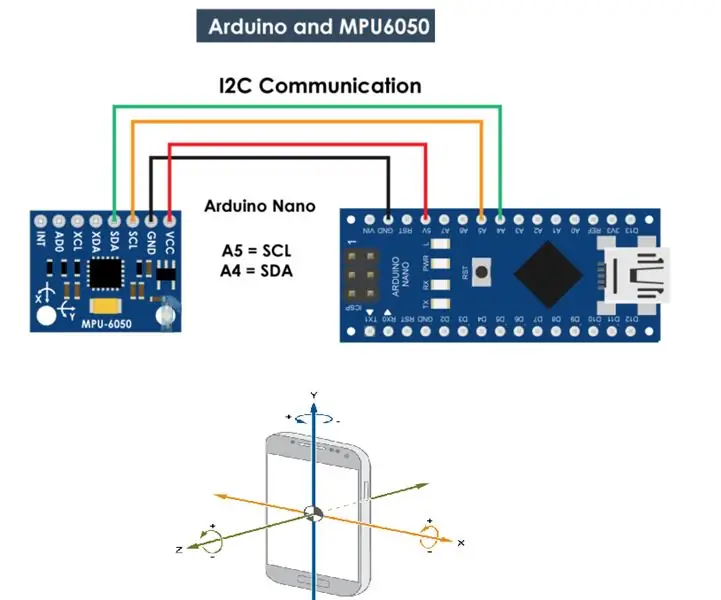
MPU 6050 giroszkóp, gyorsulásmérő kommunikáció az Arduino-val (Atmega328p): Az MPU6050 IMU 3 tengelyes gyorsulásmérőt és 3 tengelyes giroszkópot tartalmaz egyetlen chipen. A giroszkóp méri a szöghelyzet forgási sebességét vagy változási sebességét az idő mentén, a X, Y és Z tengely. A giroszkóp kimenetei
Xbox 360 vezérlő gyorsulásmérő/giroszkóp Kormányzási mód: 7 lépés

Xbox 360 vezérlő gyorsulásmérő/giroszkóp Kormányzási mód: Az Assetto Corsát játszottam az Xbox 360 vezérlőmmel. Sajnos az analóg pálcával való kormányzás nagyon nehézkes, és nincs helyem a kerék beállításához. Próbáltam elgondolkodni azon, hogyan lehetne jobb kormányművet cipelni a
MPU6050-Gyorsulásmérő+giroszkóp érzékelő alapjai: 3 lépés

MPU6050-gyorsulásmérő+giroszkóp érzékelő alapjai: Az MPU6050 nagyon hasznos érzékelő. Az mpu 6050 egy IMU: Az inerciális mérőegység (IMU) egy elektronikus eszköz, amely méri és jelenti a test sajátos erejét, szögsebességét és néha az irányt a test kombinációjával
SmartPhone Game Simulator- Játsszon Windows játékokkal az IMU gesztusvezérlés, gyorsulásmérő, giroszkóp, magnetométer segítségével: 5 lépés
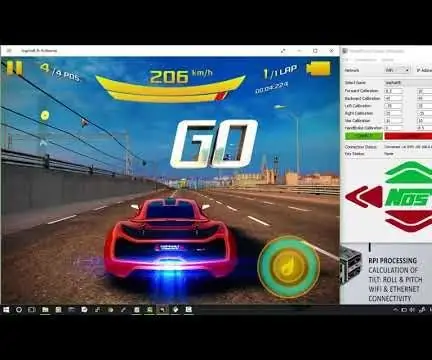
SmartPhone Game Simulator- Játsszon Windows játékokat gesztusvezérléssel IMU, gyorsulásmérő, giroszkóp, magnetométer: Támogassa ezt a projektet: https://www.paypal.me/vslcreations, adományozva nyílt forráskódoknak és & további fejlődés támogatása
Arduino Nano: gyorsulásmérő giroszkóp iránytű MPU9250 I2C érzékelő Visuino -val: 11 lépés
Arduino Nano: Gyorsulásmérő giroszkóp iránytű MPU9250 I2C érzékelő Visuino -val: Az MPU9250 az egyik legfejlettebb kombinált gyorsulásmérő, giroszkóp és iránytű kis méretű érzékelő. Számos fejlett funkcióval rendelkeznek, beleértve az aluláteresztő szűrést, a mozgásérzékelést és még egy programozható speciális processzort is
