Tartalomjegyzék:
- Szerző John Day [email protected].
- Public 2024-01-31 10:20.
- Utoljára módosítva 2025-01-23 14:48.
A PT100 egy ellenálláshőmérséklet -érzékelő (RTD), amely a környezeti hőmérséklettől függően megváltoztatja ellenállását, széles körben használják lassú dinamikájú és viszonylag széles hőmérséklettartományú ipari folyamatokhoz. Lassú dinamikus folyamatokhoz használják, mert a RTD -k lassú válaszidővel rendelkeznek (amelyekről később még beszélek), de pontosak és idővel alacsonyak. Amit ebben az utasításban mutatok nektek, az nem felel meg az ipari szabványnak, de alternatív módon teszi lehetővé a hőmérséklet mérését, mint az LM35 használata, amelyet sok hobbi ismer, és a bemutatott áramkör -elmélet más érzékelőkre is alkalmazható.
1. lépés: Alkatrészek
1x PT100 (két vezeték)
1x Arduino (bármilyen modell)
3x 741 működési erősítő (LM741 vagy UA741)
1x 80ohm ellenállás
2x 3,9 khm -os ellenállás
2x 3,3 khm -os ellenállás
2x 8,2 khm -os ellenállás
2x 47kohm ellenállás
1x 5 khm potenciométer
1x két terminálos tápegység vagy 8x 1,5V AA elem
Kétvezetékes PT100 -at használok, három- és négyvezetékes PT100 -asok különböző áramkörökkel rendelkeznek. A legtöbb ilyen ellenállás értékének nem kell pontosan megegyeznie a fentiekkel, de ha van egy pár ellenállás, azaz a 3,9 ohm, ha kicserélte őket mondjuk 5 ezerre, akkor mindkettőt le kell cserélni 5 ezerre. ugyanolyannak kell lennie. Amikor megkapjuk az áramkört, elmondom a különböző értékek kiválasztásának hatását. A műveleti erősítőkhöz (op erősítők) más op erősítőket is használhat, de ezeket én használtam.
2. lépés: Wheatstone híd
Először beszélnem kell a képlettel, hogy a hőmérsékletet a PT100 ellenállásából kapjuk, mielőtt az áramkör első részéről beszélek, az ellenállás képlete a következő:
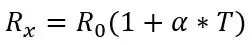
ahol Rx a PT100 ellenállás, R0 a PT100 ellenállás 0 ° C -on, α a hőmérsékleti ellenállási együttható és T a hőmérséklet.
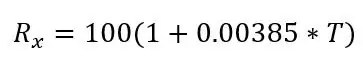
R0 100 ohm, mivel ez egy PT100, ha PT1000 lenne, akkor R0 1000 ohm lenne. α az adatlapból vett 0,00385 ohm/C fok. Van itt egy pontosabb képlet is, de a fenti képlet megfelel ennek a projektnek. Ha átültetjük a képletet, akkor kiszámíthatjuk az adott ellenállás hőmérsékletét:
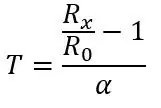
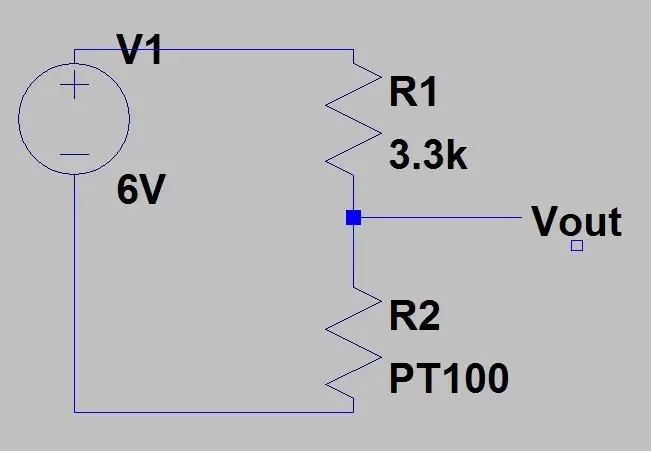
Tegyük fel, hogy valamit meg akarunk mérni, amelynek hőmérsékleti tartománya -51,85 és 130 ° C között van, és a PT100 -at az 1. ábrán látható áramkörbe helyeztük. A fenti egyenlet és a feszültségosztóból származó feszültség egyenletének használatával az első képen) kiszámíthatjuk a feszültségtartományt. A tartomány alsó része T = -51.85 (80ohms)
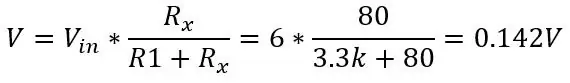
és 130 fokon (150 ohm):
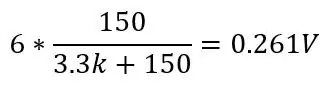
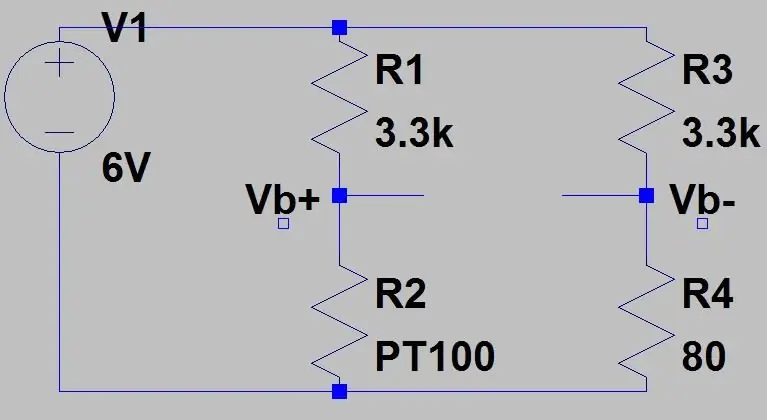
Ez 0,1187 V tartományt és 0,142 egyenáramú eltolást eredményezne, mivel tudjuk, hogy a hőmérsékletünk soha nem lesz -51,85 ° C alatt, ez csökkenti az érzékenységet az általunk fontos tartományban (80-130 ohm), amikor ezt a feszültséget felerősítjük. Ahhoz, hogy megszabaduljunk ettől az egyenáramú eltolástól és növeljük érzékenységünket, használhatunk egy Wheatstone hidat, amely a második képen látható.
A második feszültségosztó (Vb-) kimenetét később differenciális erősítővel vonják le az első feszültségosztó kimenetből (Vb+). A híd kimenetének képlete csak két feszültségosztó:
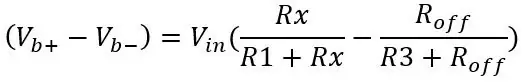
A PT100 kimeneti feszültsége 80 ohm, és a kép többi értékét használja:
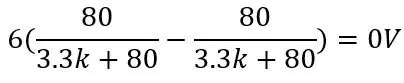
és ha a Pt100 150 ohm:
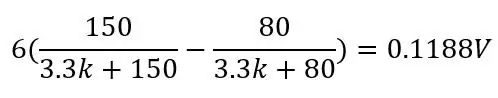
A Wheatstone használatával megszabadulunk a DC eltolástól és növeljük az érzékenységet az erősítés után. Most, hogy tudjuk, hogyan működik a Wheatstone -híd, beszélhetünk arról, hogy miért használunk 80 ohmot és 3,3 khm -ot. A 80ohm -ot a fenti képlet magyarázza, válassza ezt az értéket (ezt Roff offset ellenállásnak nevezzük), hogy a hőmérséklet alsó tartománya legyen, vagy még jobb, kissé a tartománya alja alatt, ha ezt használja A hőmérséklet -szabályozó vezérlőrendszerekhez vagy ehhez hasonlókhoz szeretné tudni, hogy a hőmérséklet mennyire csökken a hőmérsékleti tartománya alá. Tehát ha -51,85 ° C a tartomány alsó része, használjon 74,975 ohm (-65 ° C) értéket a Roff -hoz.
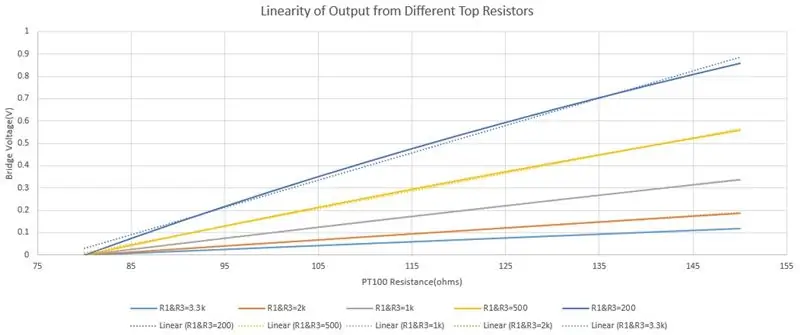
Két okból választottam a 3.3k -t az R1 és az R3 számára, hogy korlátozzam az áramot és növeljem a kimenet linearitását. Mivel a PT100 megváltoztatja az ellenállást a hőmérséklet hatására, túl sok áram átengedése hibás leolvasást eredményez az önmelegítés miatt, ezért 5-10 mA maximális áramot választottam. Ha a PT100 80 ohm, akkor az áram 1,775 mA, tehát biztonságosan a maximális tartomány alatt. Csökkenti az ellenállást az érzékenység növelése érdekében, de ez negatív hatással lehet a linearitásra, mivel később egy egyenlet egyenletét fogjuk használni (y = mx+c), ha a nemlineáris kimenet hibákat okoz. A harmadik képen grafikon látható a híd kimenetéről, különböző felső ellenállások használatával, a folytonos vonal a tényleges kimenet, a szaggatott vonal pedig a lineáris közelítés. Látható a sötétkék grafikonon (R1 és R3 = 200ohm) adja a legnagyobb feszültségtartományt, de a kimenet a legkevésbé lineáris. A világoskék (R1 és R3 = 3,3 khm) adja a legkisebb feszültségtartományt, de a szaggatott vonal és a folytonos vonal átfedésben van, ami azt mutatja, hogy linearitása nagyon jó.
Nyugodtan módosítsa ezeket az értékeket az alkalmazásának megfelelően, ha a feszültséget is megváltoztatja, ügyeljen arra, hogy az áram ne legyen túl magas.
3. lépés: Erősítés
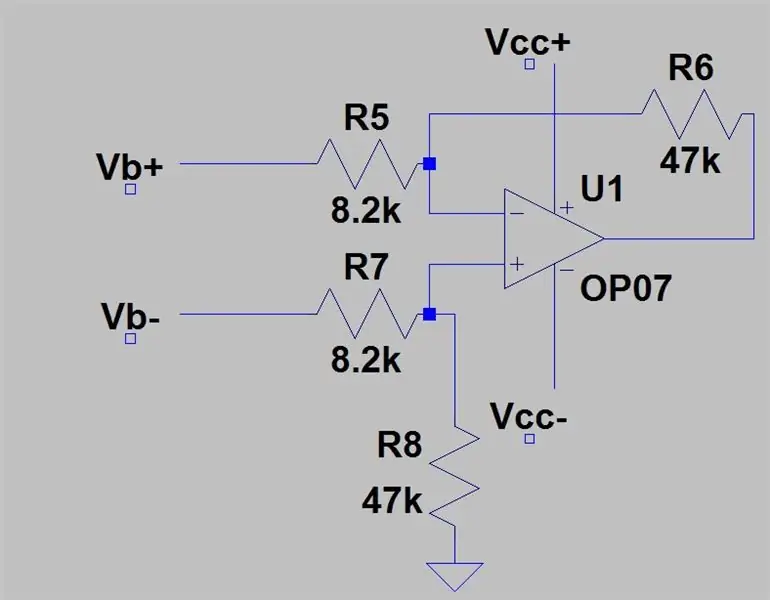
Az utolsó lépésben azt találtuk, hogy a levont két feszültségosztó kimeneti tartománya 0 és 0.1187 között van, de nem beszéltünk arról, hogyan lehet ezeket a feszültségeket levonni. Ehhez szükségünk lesz egy differenciális erősítőre, amely kivonja az egyik bemenetet a másikból, és ezt erősíti az erősítő erősítésével. A differenciálerősítő áramköre az első képen látható. A Vb+ -t az invertáló bemenetbe és a Vb- a nem invertáló bemenetbe táplálja, és a kimenet a Vb+- Vb- lesz, egy erősítéssel, azaz nincs erősítés, de a képen látható ellenállások hozzáadásával 5,731 erősítést adunk. A nyereséget a következők adják:
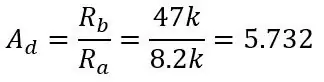
Ra R5 és R7 és Rb R6 és R8, a kimeneti feszültséget a következők adják meg:
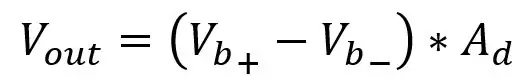
Két probléma van az erősítőnek a híd kimenetéhez való csatlakoztatásával, a terhelési effektussal és az erősítés megváltoztatásával. Az erősítő erősítésének megváltoztatásához legalább két ellenállást kell cserélnie, mivel a két ellenálláspárnak azonosnak kell lennie, így két edény, amelyeknek azonos értékűnek kell lenniük, bosszantó lenne, ezért valami úgynevezett műszeres erősítőt használunk amelyekről alább beszélek. A terhelési hatás az erősítő bemeneti ellenállása, amely befolyásolja a PT100 feszültségcsökkenését, azt akarjuk, hogy a PT100 feszültsége változatlan maradjon, és ehhez nagyon nagy ellenállásokat választhatunk a bemeneti ellenállásokhoz, hogy a PT100 párhuzamos ellenállása és a bemeneti ellenállás nagyon közel van a PT100 ellenálláshoz, de ez problémákat okozhat a zaj és a feszültség kimeneti eltolásában, amelyekbe nem megyek bele. Csak válassza a Kohms tartomány középső tartományát, de mint mondtam, a kis ellenállások is rosszak, ezért változtatunk egy kicsit az áramkörön.
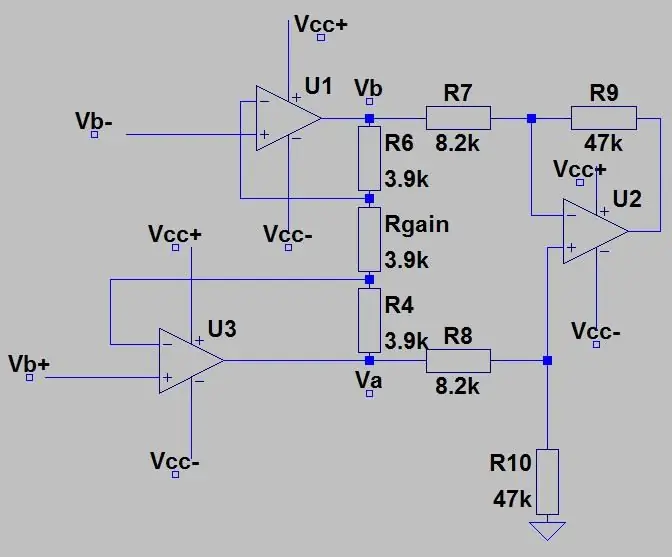
A második képen a híd kimenete egy műszeres erősítőhöz van csatlakoztatva, amely puffer erősítőt választ el az áramkörök két felének (a híd és az erősítés) szétválasztására, valamint lehetővé teszi a bemenet erősítését egy potenciométer megváltoztatásával (Rgain). A műszeres erősítő nyeresége a következő:
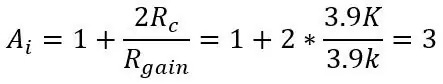
ahol Rc a két 3,9 k ellenállás az edény felett és alatt.
Az Rgain csökkentésével az erősítés nő. Aztán a Va és Vb pontban (erősített Vb+ és Vb-) ez csak egy differenciális erősítő, mint korábban, és az áramkör teljes nyeresége csak a nyereség együttes szorzata.
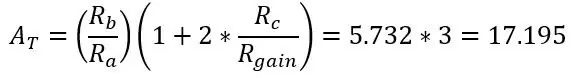
A nyereség kiválasztásához olyasmit szeretne csinálni, mint korábban a Roff esetében, válasszunk egy ellenállást, amely éppen meghaladja a maximális hőmérsékletet a tartományban, arra az esetre, ha ez meghaladná. Mivel az Arduino -t használjuk, amelynek 5 V -os adc -ja van, az áramkör maximális kimenetének 5 V -nak kell lennie a kiválasztott maximális hőmérsékleten. Válasszuk ki a 150ohm-ot, mint a maximális ellenállást, és a híd feszültsége nem erősítve 0.1187V volt, a szükséges erősítés 42.185 (5/0.1187)
Tegyük fel, hogy Ra, Rb és Rc értéke 8,2k, 47k és 3,9k, csak meg kell találnunk az Rgain pot értékét:
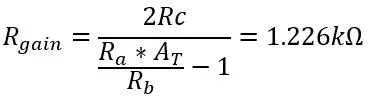
Tehát, hogy a teljes 5 voltot kihozza az általunk használt hőmérsékleti tartományból, módosítsa az Rgain értékét 1,226k -ra. A differenciális erősítőből kilépő kimeneti feszültséget a következők adják meg:
4. lépés: Az áramkör bekapcsolása
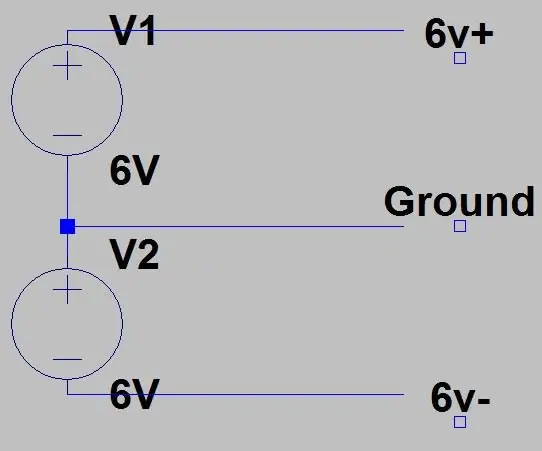

Ez az áramkör utolsó lépése, lehet, hogy észrevette a Vcc+ és a Vcc- az op erősítő áramkörökön, ez azért van, mert pozitív és negatív feszültségre is szükségük van a megfelelő működéshez, lehet kapni egy sínű op erősítőket hogy ezeket az erősítőket használjam, mert így hevertem. Tehát +6V és -6V feszültséget biztosítunk, ezt háromféleképpen tehetjük meg. Az első az első képen látható, ahol két tápegységhez vagy két kimeneti csatlakozóhoz kell csatlakoznunk egyetlen tápegységből, mindkettő 6 V feszültségű, és az egyik pozitív kimenet a másik negatívhoz van csatlakoztatva. A felső tápegység 6 V -ja a mi +6 V -os, az alsó táp pozitívja a GND, az alsó pedig a -6 V. CSAK CSATLAKOZZA Hasonló módon, HA A KÉT TÁRGY GND -je el van választva, vagy károsítja az áramellátást. Minden kereskedelmi tápegység elválasztotta volna a GND -ket, de ha ellenőrizni szeretné, használja a folytonossági tesztelőt a multiméteren, ha zümmög, ne használja ezt a beállítást, és használja a következőt. A házi készletemnél ezzel kiégettem a biztosítékot.
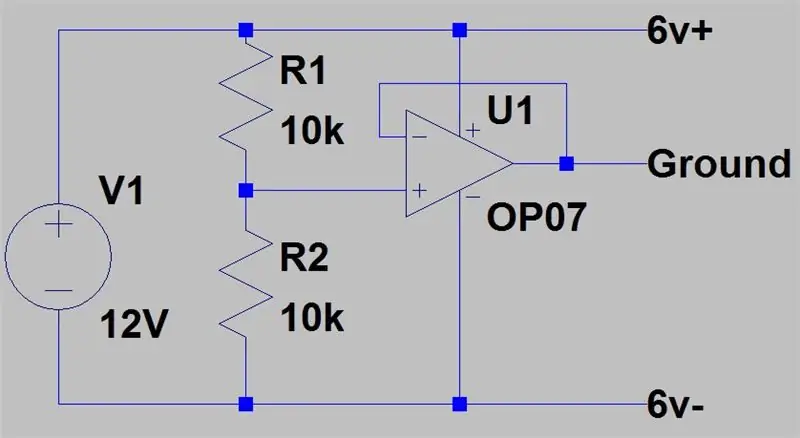
A második képen a második beállítás áll rendelkezésünkre, de az egyik tápegységnek meg kell dupláznia a másik feszültségét, de nem károsítja a tápellátást, ha a GND -k csatlakoztatva vannak. Két tápegységünk van, az egyik 12V -os, a másik 6V -os. A 12V +6V, a második tápegységből származó 6V GND, a két tényleges GND pedig -6V lesz.
Ez az utolsó beállítás a csak egy kimenettel rendelkező tápegységekre vonatkozik, 1 erősítésű puffererősítőt használ, hogy virtuális földet hozzon létre a tápfeszültség felének átvezetésével a puffer erősítőn. Ekkor a 12V +6V, a tényleges GND terminál pedig -6V lesz.
Ha elemeket szeretne használni, akkor javaslom az első beállítást, de az akkumulátorokkal az a probléma, hogy a feszültség csökkenni kezd, ahogy kezdenek meghalni, és a hídról érkező feszültség is csökkenni fog, rossz hőmérsékleti értékeket adva. Természetesen leolvashatja az akkumulátorok feszültségét, és belefoglalhatja őket a számításokba, vagy használhat szabályozókat és további elemeket. Végül csak rajtad múlik.
5. lépés: Teljes kör és kód
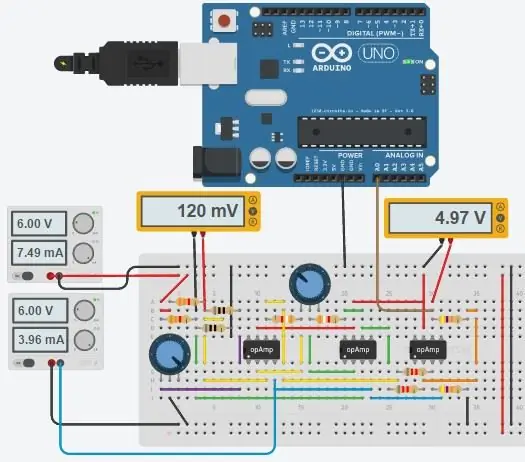
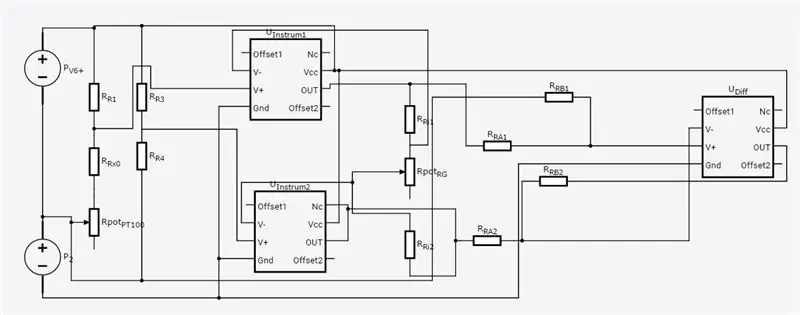
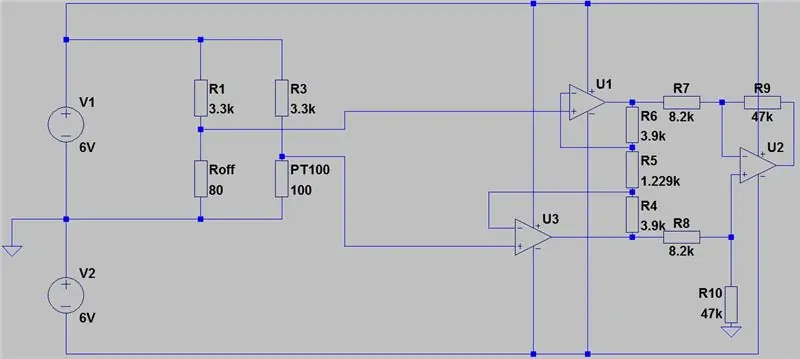
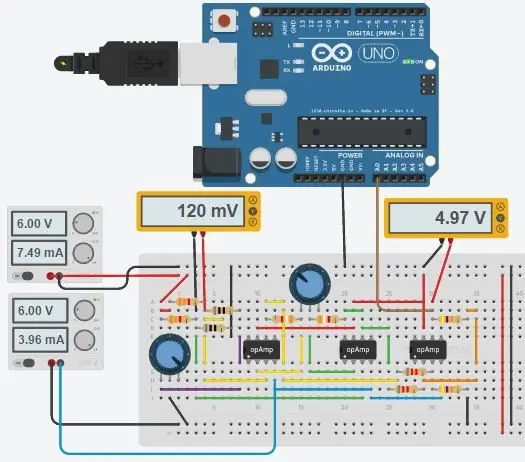
A teljes áramkör a fentiekben látható, és az Autodesk új Circuits.io -jában készült, amely lehetővé teszi áramkörök létrehozását a kenyértáblán, az áramköri diagram szerkesztését (a 2. ábrán látható) és a NYÁK -diagramokat, valamint a legjobb részt, lehetővé teszi az áramkör szimulálását a kenyértábláról és akár programozhat egy Arduino -t, és csatlakoztathatja azt a kenyértábla módban, az oldal lejjebb található a szimuláció, és két potot játszhat. Ha meg szeretné sokszorozni az áramkört és be szeretné állítani saját értékeit, akkor itt találja az áramkört. Az első edény 70 ohm, sorban egy 80 ohmos ellenállással, amely 80-150 ohm tartományban szimulálja a PT100-at, a második edény a műszeres erősítő erősítése. Sajnos a letöltött könyvtárat használtam a kódomhoz, így az Arduino nem szerepel az alábbi áramkörben, de csak két extra vezetéket kell csatlakoztatni. Ha jobban érzed magad az LTspice használatában, akkor az áramkörhöz mellékeltem egy asc fájlt.
Csatlakoztassa az A0 tűt a differenciális erősítő kimenetéhez
Csatlakoztassa az Arduino GND -jét az áramkör GND -jéhez (NEM A -6V)
És ez az áramkör kész, most a kódra. Korábban említettem, hogy az y = mx+c képletet fogjuk használni, nos, most kiszámítjuk az m (a meredekség) és a c (az eltolás) képletet. Az Arduino -ban feszültséget fogunk olvasni, de a hőmérséklet -egyenletnek meg kell ismernie a PT100 ellenállását, így ezt úgy tehetjük meg, hogy a Serial.println (temp) értéket Serial.println (V) -re cseréljük, és rögzítjük feszültség és ellenállás két hőmérsékleten. Ha ezt a tesztet végzi, hagyja a PT100 -at egy ideig, például egy -két percig, és tartsa távol minden hőforrástól (napfény, laptop ventilátora, teste stb.).
Az első pont, amit megtehetünk, a szobahőmérséklet, amikor az áramkört csatlakoztatja és működik, jegyezze fel az Arduino által leolvasott feszültséget (Vt1) a soros monitoron, és gyorsan válassza le a PT100 -at, és jegyezze fel az ellenállását (Rt1). lekapcsoláskor a kezét a szondával, mert ez megváltoztatja az ellenállást. A második hőmérsékletnél a szondát jeges vízbe vagy forró vízbe tehetjük (legyen óvatos, ha forró vizet használ), és megismételjük, amit tettünk, mielőtt megtaláltuk a Vt2 és az Rt2 értékeket. Közvetlenül a szonda folyadékba helyezése után várjon egy -két percet, amíg az ellenállás rendeződik. Ha érdekli a PT100 időreakciója, rögzítse a soros monitor feszültségét körülbelül 2 másodpercenként, és ebből grafikont rajzolhatunk, és később elmagyarázom. A két feszültség és ellenállás segítségével a meredekséget a következőképpen számíthatjuk ki:
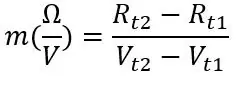
Rt1 és Rt2 az ellenállás a két hőmérsékleten, és ez igaz a Vt1 és Vt2 feszültségekre is. A meredekségből és a két rögzített ponthalmaz egyikéből kiszámíthatjuk az eltolást:
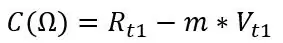
C -nek közel kell lennie a valódi Roff -hoz, a szimulációmból kiszámítottam ezeket az értékeket:
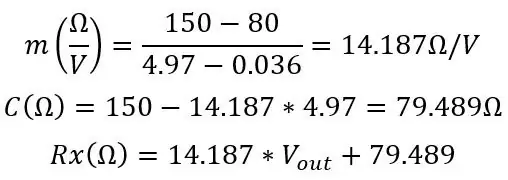
Ebből az ellenállásból a kezdetben használt képlet segítségével megtalálhatjuk a hőmérsékletünket:
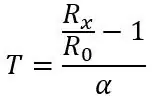
És ennyi, az Arduino kódja alább található, ha bármilyen problémája van, hagyjon megjegyzést, és megpróbálok segíteni.
Nincsenek képek arról az áramkörről, amelyet egy ideje készítettem, és a PT100 -at már nem kell újra elkészíteni és tesztelni, de el kell hinned, hogy működik. Az Instructables -en nem sokat találok a PT100 -ról, ezért találtam ezt az ible -t.
A következő lépésben a PT100 időreakciójáról fogok beszélni, és ha nem érdekli a matematika, akkor a hőmérsékletváltozás mérésekor hagyja a PT100 -at leülepedni egy percig, mielőtt leolvasná.
Ha kíváncsi vagy az általam készített egyéb projektekre, látogasd meg az én oldalamat
Blog: Roboroblog
YouTube -csatorna: Roboro
Vagy nézd meg a többi utasításomat: itt
Ha a HTML elrontja az alábbi kódot, a kód csatolva van
* Ez a kód a PT100 segítségével számítja ki a hőmérsékletet
* Írta: Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- From-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object
void setup() {
Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }
Step 6: Time Response of PT100
Tehát megemlítettem, hogy a PT100 lassú reakcióval rendelkezik, de bármikor kaphatunk egy képletet a PT100 által leolvasott aktuális hőmérsékletre t. A PT100 válasza egy elsőrendű válasz, amelyet Laplace kifejezéssel, azaz átviteli függvénnyel lehet írni:
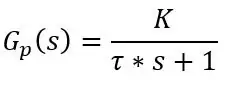
ahol tau (τ) az időállandó, K a rendszer nyeresége és s a Laplace operátor, amely jω -ként írható, ahol ω a frekvencia.
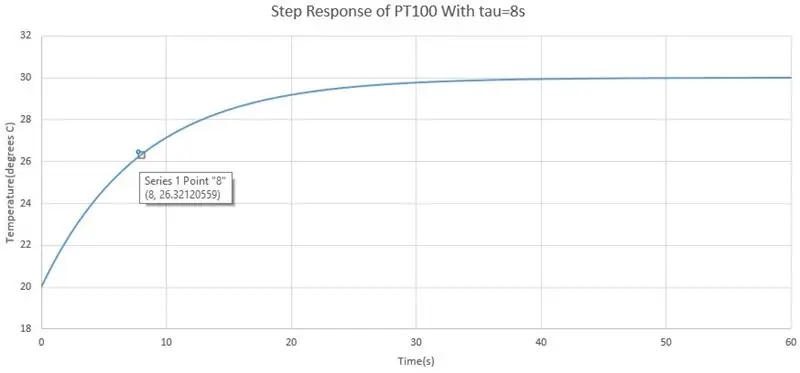
Az időállandó azt mutatja meg, hogy mennyi időbe telik az első rendű rendszer az új értéken való elhelyezkedéshez, és az a szabály vagy hüvelykujj, hogy az 5*tau az, hogy mennyi idő alatt rendeződik az új egyensúlyi állapotban. A K erősítés megmutatja, hogy a bemenet mennyit erősít. A PT100 esetében a nyereség az, hogy az ellenállásváltozások mennyit osztanak a hőmérsékletváltozással, két véletlen érték kiválasztásából ebből az adatlapból 0,3856 ohm/C erősítést kaptam.
Mielőtt azt mondtam, hogy a feszültséget 2 másodpercenként rögzítheti, miután a szondát folyadékba helyezte, meleg vagy hideg, ebből kiszámíthatjuk a rendszer időállandóját. Először meg kell határoznia, hol van a kiindulópont és a végpont, a kezdőpont a feszültség, mielőtt a szondát a folyadékba helyezi, a végpont pedig az, amikor leülepedett. Ezután vonja le őket, és ez a lépés feszültségváltozása. Az elvégzett teszt egy lépésváltozás volt, amely hirtelen változás a rendszer bemenetében, a lépés a hőmérséklet. Most a grafikonon menjen a feszültségváltozás 63,2% -ára, és ez az időállandó.
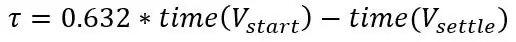
Ha ezt az értéket csatlakoztatja az átviteli függvényhez, akkor megvan a képlet, amely leírja a rendszerek frekvenciaválaszát, de ez nem az, amit most szeretnénk, hanem a t időbeli tényleges hőmérsékletet szeretnénk egy hőmérsékleti lépésre. hogy egy lépés inverz Laplace -transzformációját kell végrehajtania a rendszerbe. Az elsőrendű rendszer átviteli funkciója egy lépés bemenetével a következő:
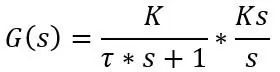
Ahol Ks a lépés mérete, azaz a hőmérséklet különbség. Tegyük fel, hogy a szondát 20 ° C -on ülepítjük, 30 ° C -os vízbe helyezzük, és a szonda időállandója 8 s, az átviteli függvény és az időtartomány képlete a következő:
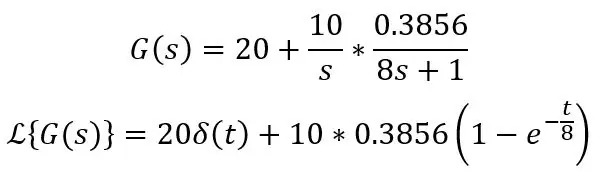
A δ (t) ebben az esetben csak impulzus, azaz egyenáramú 20 ° C -eltolást jelent, ennek kiszámításakor csak 20 -at írhat az egyenleteibe. Ez a standard egyenlet az első rendű rendszerbe lépéshez:
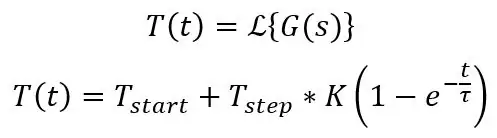
A fentiek kiszámítják a hőmérsékletet a t időpontban, de ez működni fog a feszültségnél, mivel arányosak egymással, csak a kezdő és befejező értékre, az időállandóra és a lépésméretre van szükség. A Symbolab nevű webhely kiválóan alkalmas annak ellenőrzésére, hogy helyes -e a matematikája, képes -e Laplace -re, integrációra, differenciálásra és még sok mindenre, és megadja az összes lépést az út mentén. A fenti fordított Laplace -transzformáció itt található.
Ajánlott:
Hőmérséklet és páratartalom mérése DHT11 / DHT22 és Arduino használatával: 4 lépés

Hőmérséklet és páratartalom mérése a DHT11 / DHT22 és az Arduino használatával: Ebben az Arduino bemutatóban megtanuljuk, hogyan kell használni a DHT11 vagy a DHT22 érzékelőt a hőmérséklet és páratartalom mérésére az Arduino táblával
Hőmérséklet mérése ADT75 és Arduino Nano használatával: 4 lépés

Hőmérsékletmérés az ADT75 és az Arduino Nano segítségével: Az ADT75 egy rendkívül pontos, digitális hőmérséklet -érzékelő. Tartalmaz egy sávköz-hőmérséklet-érzékelőt és egy 12 bites analóg-digitális átalakítót a hőmérséklet figyelésére és digitalizálására. Rendkívül érzékeny érzékelője kellően hozzáértővé teszi számomra
Hőmérséklet és páratartalom mérése HDC1000 és Arduino Nano használatával: 4 lépés
Hőmérséklet és páratartalom mérése HDC1000 és Arduino Nano használatával: A HDC1000 egy digitális páratartalom -érzékelő beépített hőmérséklet -érzékelővel, amely kiváló mérési pontosságot biztosít nagyon alacsony teljesítmény mellett. A készülék egy új kapacitív érzékelő alapján méri a páratartalmat. A páratartalom és a hőmérséklet érzékelők
Hőmérséklet mérése AD7416ARZ és Arduino Nano használatával: 4 lépés
Hőmérsékletmérés az AD7416ARZ és az Arduino Nano használatával: Az AD7416ARZ 10 bites hőmérséklet-érzékelő négy egycsatornás analóg-digitális átalakítóval és egy beépített hőmérséklet-érzékelővel. Az alkatrészek hőmérséklet -érzékelője multiplexer csatornákon keresztül érhető el. Ez a nagy pontosságú hőmérséklet
Hőmérséklet mérése PT100 és Arduino segítségével: 16 lépés
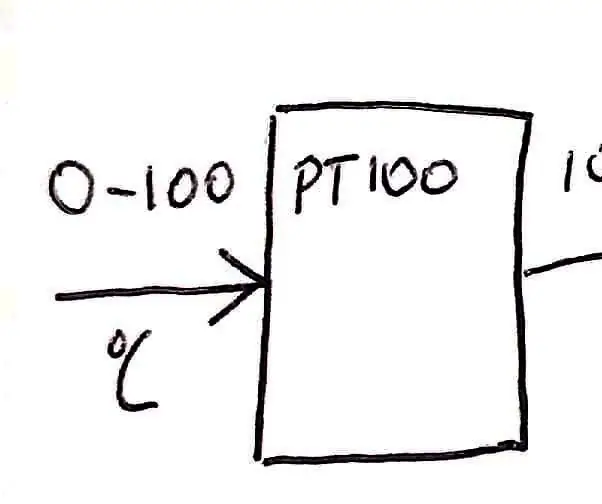
Hőmérséklet mérése PT100 és Arduino segítségével: A projekt célja egy hőmérsékletérzékelő rendszer megtervezése, kivitelezése és tesztelése. A rendszert 0 és 100 ° C közötti hőmérséklettartomány mérésére tervezték. A PT100 -at használták a hőmérséklet mérésére, és ez egy ellenálláshőmérséklet -érzékelő (RTD)
