Naprendszer szimuláció: 4 lépés

2024 Szerző: John Day | [email protected]. Utoljára módosítva: 2024-01-30 09:42

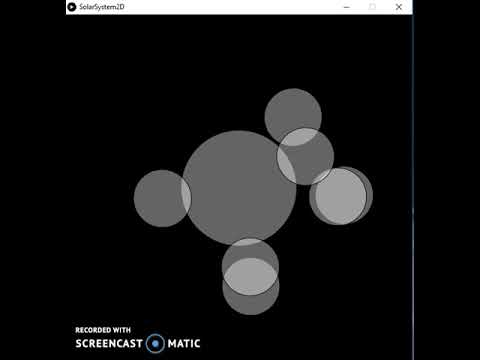
Ehhez a projekthez szimulációt készítettem arról, hogy a gravitáció hogyan befolyásolja a Naprendszer bolygótesteinek mozgását. A fenti videóban / a Nap testét a drótháló gömb képviseli, és a bolygók véletlenszerűen keletkeznek.

A bolygók mozgása a valódi fizikán, az egyetemes gravitáció törvényén alapul. Ez a törvény határozza meg a gravitációs erőt, amelyet egy másik tömeg okoz egy tömegre; ebben az esetben a Nap az összes bolygón, és a bolygók egymáson.

Ehhez a projekthez a Processing, egy java alapú programozási környezetet használtam. A feldolgozás példafájlját is használtam, amely a bolygók gravitációját szimulálja. Ehhez csak egy feldolgozó szoftverre és egy számítógépre lesz szüksége.

1. lépés: 2 Dimenziós szimuláció

Először néhány videót néztem meg arról, hogyan kell kódolni, amit Dan Shiffman készített a YouTube -csatornáján, a Coding Train -ban (1/3. Rész). Ezen a ponton azt gondoltam, hogy rekurziót fogok használni a Naprendszer előállításához, hasonlóan ahhoz, ahogy Shiffman csak a fizika törvényeit használja.

Létrehoztam egy bolygóobjektumot, amelynek „gyermekbolygói” voltak, és akiknek „gyermekbolygói” is voltak. A 2D szimuláció kódja nem fejeződött be, mert nem volt nagyszerű módom az egyes bolygók gravitációs erőinek szimulálására. Ebből a gondolkodásmódból tértem ki, a gravitációs vonzás beépített feldolgozási példáján alapuló irányba. A probléma az volt, hogy ki kellett számolnom a gravitációs erőt az összes bolygó minden bolygójáról, de nem tudtam elképzelni, hogyan lehet egyszerűen begyűjteni az egyes bolygók információit. Miután láttam, hogy a Processing bemutató hogyan csinálja, rájöttem, hogy pontosan hogyan kell ezt csinálni hurkok és tömbök használatával

2. lépés: Három dimenzióba állítása

A feldolgozáshoz tartozó Planetary Attraction példakódjával új programot indítottam el egy 3D szimulációhoz. A fő különbség a Planet osztályban van, ahol hozzáadtam egy vonzó függvényt, amely kiszámítja a két bolygó közötti gravitációs erőt. Ez lehetővé tette számomra, hogy szimuláljam a naprendszereink működését, ahol a bolygókat nemcsak a nap vonzza, hanem minden más bolygó is.

Minden bolygónak vannak véletlenszerűen generált jellemzői, például a tömeg, a sugár, a pálya kezdeti sebessége, stb. Ezenkívül a kamera helye az ablak közepén forog.

3. lépés: Valódi bolygók használata

Miután leszereltem a 3D szimuláció keretét, a Wikipédia segítségével megkerestem a Naprendszerünk tényleges bolygóadatait. Létrehoztam egy sor bolygó objektumot, és bevittem a valós adatokat. Amikor ezt megtettem, le kellett skáláznom az összes jellemzőt. Amikor ezt megtettem, akkor a tényleges értékeket kellett volna vennem, és szorozniuk egy tényezővel az értékek csökkentéséhez, ehelyett a Föld egységeiben tettem. Vagyis a Föld értékét a többi tárgy értékéhez vettem, például a Napnak 109 -szer nagyobb a tömege, mint a Földnek. Ez azonban azt eredményezte, hogy a bolygók mérete túl nagynak vagy túl kicsinek tűnt.

4. lépés: Utolsó gondolatok és megjegyzések

Ha tovább dolgoznék ezen a szimuláción, néhány dolgot finomítanék/javítanék:

1. Először mindent egységesen skáláznék ugyanazzal a skálázási tényezővel. Aztán hogy javítsam a pályák láthatóságát, minden bolygó mögött nyomvonalat adnék, hogy lássam, hogyan viszonyul minden egyes forradalom az előzőhöz

2. A kamera nem interaktív, ami azt jelenti, hogy a pályák egy része kívül van a képernyőn, "a személy mögött". Van egy Peazy Cam nevű 3D kamerakönyvtár, amelyet a Coding Train ebben a témában készült videósorozatának 2. részében használnak. Ez a könyvtár lehetővé teszi a néző számára, hogy forgassa, pásztázza és nagyítsa a kamerát úgy, hogy képes legyen követni a bolygó teljes pályáját.

3. Végül, a bolygók jelenleg megkülönböztethetetlenek egymástól. Szeretnék minden bőrhöz és Naphoz „bőrt” hozzáadni, hogy a nézők felismerjék a Földet és hasonlókat.