
Tartalomjegyzék:
- Szerző John Day [email protected].
- Public 2024-01-30 09:41.
- Utoljára módosítva 2025-01-23 14:47.

Mind a 7 alapvető logikai kapu elkészítése Excelben nem túl nehéz. Ha megérti az Excel funkcióit, akkor ez a projekt meglehetősen egyszerű lenne, ha nem, nem kell aggódnia, nem kell sokáig megszoknia.
Az Excel már létrehozott nekünk néhány logikai kaput, de nem tartalmazza mind a 7 -et, és mi mindenképpen magunk szeretnénk elkészíteni.
A projekt nem tart sokáig, és miután elkészült, számos áramkört létrehozhat digitálisan az Excelben.
1. lépés: Amire szüksége van
Ehhez a projekthez nem kell sok.
- Számítógép
- Excel (az Excel -t ajánlom, de a hasonlóaknak is megfelelőnek kell lenniük)
- Alapvető ismeretek a logikai kapuk működéséről
2. lépés: Az Excel és a formátum beállítása

Először indítsa el az Excel programot (A verzió nem sokat számít, de az Excel 2016 -ot használtam), majd nyisson meg egy új "Üres munkafüzetet".
Ezután készítse el a fenti képen látható formátumot (A kép formája miatt rá kell kattintania a megfelelő megtekintéshez, ez a következő képekre vonatkozik). Ha nem tudja másolni a formátumot, olvassa el az alábbiakat:
Tegye a B & C oszlopot egy számjegy szélességűvé, egyesítse az 1. A, B & C sort.
Ezután írja be a szöveget.
3. lépés: ÉS kapu
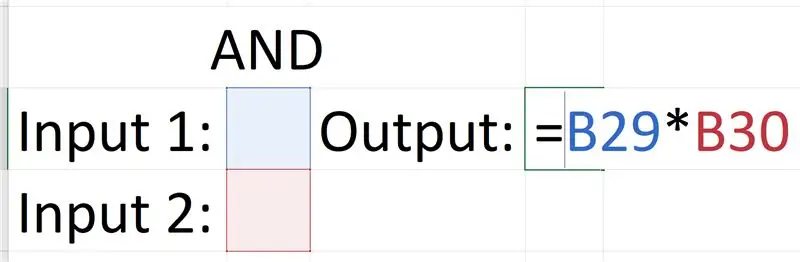
Az ÉS kapu a legegyszerűbb, ez azért van, mert a kimenetet csak a bemenetek megszorzásával kaphatja meg.
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1
Ez az egyenlet szorzata megegyezik a kapu kimeneteivel.
Másolja le a képletet és tesztelje a bemenetek megadásával (csak bináris formában).
Ne feledje, minden alkalommal, amikor új kaput hoz létre, másolja az elrendezést, hogy semmi ne legyen átfedésben.
4. lépés: VAGY kapu
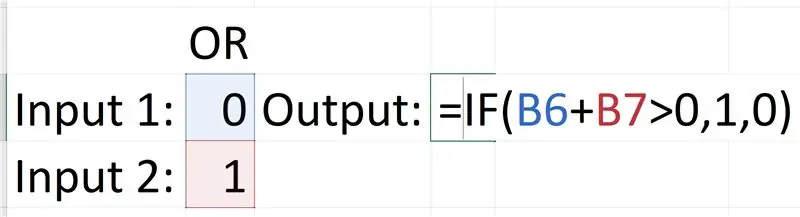
A VAGY kapu bonyolultabb, ehhez „Ha” utasítás szükséges. Az 'If' utasítás így működik: = Ha (logikai_teszt, [érték, ha igaz], [érték hamis]). Az általunk használt logikai teszt a következő: Input1 + Input2> 0, a valódi érték 1, ellenkező esetben az érték 0. Ez azért van, mert csak ha mindkét bemenet hamis, a kimenet hamis lesz, és mivel 0 + 0 = 0, bármi az 1 -et tartalmazó bemenetkészlet értéke nagyobb (összegek értéke). Tehát ha mindkét bemenet összege nagyobb, mint 0, akkor a kimenete igaz vagy 1.
5. lépés: NAND Gate

A NAND kapu olyan, mint a VAGY kapu, megköveteli az „If” utasítást, és a mögötte lévő logika hasonló. A kapu csak hamis kimenetet ad, ha mindkét bemenet igaz. Tehát ha mindkét bemenetet megszorozzuk, minden 1 -nél kisebb összeg igaz lesz, mert az "If" utasítás: input1 x input2 <1, 1, 0. Ha ez zavaró volt, akkor ez a diagram segíthet:
0 x 0 = 0, 0 <1 tehát igaz = 1
0 x 1 = 0, 0 <1, így igaz = 1
1 x 0 = 0, 0 <1 tehát igaz = 1
1 x 1 = 1, 1 = 1, tehát hamis = 0
6. lépés: NOR kapu

A NOR kapu „If” utasítást is használ, ennek a kapunak az állítása: Input1 + Input2 <1, 1, 0. Ez azért van, mert a kapu csak True kimenetet ad mindkét bemenet hamis. Mivel mindkét bemenetet összeadjuk, az 1 -et tartalmazó bemenetek bármelyike nagyobb lesz, mint két 0s. Ekkor az Igaz és hamis állítás azt mutatja, hogy ha bármelyik összeg kisebb, mint 1, akkor az 1 mutatása különben 0 -t mutat.
0 + 0 = 0, 0 <1 tehát igaz = 1
0 + 1 = 1, 1 = 1, tehát hamis = 0
1 + 0 = 1, 1 = 1, tehát hamis = 0
1 + 1 = 2, 2> 1, tehát hamis = 0
7. lépés: XOR -kapu

Ez nagyon hasonló a NOR kapuhoz, de ahelyett, hogy nagyobb vagy kevesebb szimbólumot használnánk, egyenlőségjelet használunk, mert a kapu csak akkor ad ki valódi kimenetet, ha vegyes bemenete van, tehát ha mindkét bemenetet összeadjuk, vegyes bemeneteket adunk hozzá mindig 1 -et ad, így a következőt használjuk: Input1 + Input2 = 1, 1, 0.
0 + 0 = 0, 0 ≠ 1 tehát hamis = 0
0 + 1 = 1, 1 = 1, így igaz = 1
1 + 0 = 1, 1 = 1 tehát igaz = 1
1 + 1 = 2, 2 ≠ 1 tehát hamis = 0
8. lépés: XNOR Gate

Az XNOR kapu meglehetősen egyszerű, alapvetően az XOR kapu ellentéte, ez azt jelenti, hogy a logikai teszt az ellenkezője is. Ez a kapu csak akkor ad ki igaz kimenetet, ha mindkét bemenet azonos számú, vagyis bármely vegyes bemenethalmaz hamis. Az XOR kapu logikai tesztje: Input1 + Input2 = 1, de az XNOR kapu logikai tesztje: Input1 + Input2 ≠ 1. (az Excel képletekben ≠).
0 + 0 = 0, 0 ≠ 1 tehát igaz = 1
0 + 1 = 1, 1 = 1, tehát hamis = 0
1 + 0 = 1, 1 = 1, tehát hamis = 0
1 + 1 = 2, 2 ≠ 1 tehát igaz = 1
9. lépés: NEM kapu

A NOT kapu egyszerű kapu, de az „If” kijelentése ugyanaz, mint a többi. Csak egy bemenetet tartalmaz, ezért érdemes megváltoztatni a formátumot. A kapu csak megfordítja a bemenetét, így a képlet nem olyan nehéz, a logikai teszt a következő: ha a bemenet 0, és a True állítás: 1. kijelző, különben 0.
0 = 0, tehát igaz = 1
1 ≠ 0, tehát hamis = 0
10. lépés: Digitális logikai áramkör

Miután létrehozta az összes logikai kaput, ezek segítségével logikai áramköröket készíthet az Excelben. De a jelenlegi formátum túl nagy, így kipróbálhatja az új formátumot (fenti kép).
Készítsen két oszlopot egy számjegy szélesre, egyesítse a felső két cellát a kimeneti kijelző létrehozásához, az alsó két cella pedig bemenet.
A képlet beírásakor írja be a kívánt kapu képletét a kimeneti megjelenítési helyre.
11. lépés: Hibaelhárítás
Ha a logikai kapu bármelyik szakaszában nem működik megfelelően, győződjön meg arról, hogy a képletet helyesen gépelte be, és hogy a bemenetek megfelelően kapcsolódtak a képlethez.
Ha biztos abban, hogy minden helyes, akkor lehet, hogy hibát követtem el, amikor ezt az utasítást írtam, ha igen, kérjük, mondja el megjegyzésekben, hogy javíthassak.
Ajánlott:
Logikai kapuk a tranzisztor használatával: 3 lépés

Logikai kapuk a tranzisztor használatával: A logikai kapuk minden digitális rendszer alapvető építőkövei
A T Distribution használata az Excelben: 8 lépés
A T Distribution használata az Excelben: Ez az útmutató egyszerű magyarázatot és bontást nyújt a T Distribution Excelben történő használatáról. Az útmutató elmagyarázza, hogyan kell telepíteni az adatelemző eszközcsomagot, és megadja az Excel szintaxisát hat típusú T-elosztási funkcióhoz, nevezetesen: Bal oldali T Dis
Termékáramkör logikai kapuk használatával: 4 lépés
Termékösszeg áramköre logikai kapuk használatával: Ebben az oktatóanyagban megmutatom, hogyan hozhat létre saját rendszert a termékek összegének, egy kis Boole -algebrának és néhány logikai kapun keresztül. Nem ugyanazt a rendszert kell létrehoznia, mint az oktatóanyagban, de használhatja a
Hogyan készítsünk makrót az Excelben, és másoljuk az adatokat egyszerűbb módon: 4 lépés

Hogyan készítsen makrót Excelben és másolja az adatokat egyszerűbben: Szia, ez az utasítás megtanítja a makró egyszerű és jobb létrehozásának módját az adatok másolásához és beillesztéséhez, amelyek példaként fognak megjelenni
Kettős logikai tranzisztoros kapuk: 10 lépés
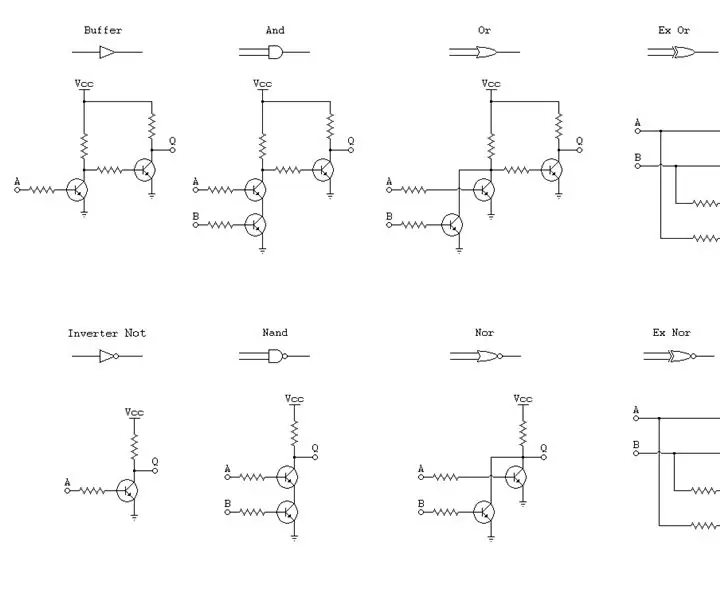
Kettős logikai tranzisztoros kapuk: A tranzisztor kapukat egy kicsit másképp építem, mint a legtöbb más elektronikai mérnök. A legtöbb ember, amikor tranzisztoros kapukat épít; csak pozitív logikát szem előtt tartva építsék fel őket, azonban az IC -k kapui két logikával rendelkeznek, a pozitív és a negatív logikával. A
