
Tartalomjegyzék:
- 1. lépés: Az algoritmus megértése 1. rész: A határozott integrál és használata
- 2. lépés: Az algoritmus megértése 2. rész: Numerikus közelítés
- 3. lépés: Az algoritmus megértése 3. rész: A középpont szabály
- 4. lépés: A program létrehozása 1. rész: Python fordító/szerkesztő letöltése
- 5. lépés: A program létrehozása 2. rész: Funkciók importálása és változók meghatározása
- 6. lépés: A program létrehozása 3. rész: Integrációs függvény létrehozása
- 7. lépés: A program létrehozása 4. rész: A válasz megjelenítése
- 8. lépés: A program futtatása 1. rész: A program futtatása úgy, ahogy van
- 9. lépés: A program futtatása 2. rész: Más matematikai függvények integrálása
- 10. lépés: A program futtatása 3. rész: A program kibővítése
- Szerző John Day day@howwhatproduce.com.
- Public 2024-01-30 09:43.
- Utoljára módosítva 2025-01-23 14:48.

Ez egy oktatóanyag arról, hogyan lehet létrehozni és futtatni egy programot, amely számszerű integrációs algoritmus segítségével értékeli a meghatározott integrálokat. A lépéseket 3 részre osztottam: a program elkészítéséhez használt algoritmus megértése, a program kódolása a Python programozási nyelv használatával és a program futtatása. Ez az oktatóanyag azoknak készült, akiknek szükségük lehet egy gyors számológép elkészítésére a meghatározott integrálok értékeléséhez, vagy esetleg szüksége van az algoritmusra egy nagyobb méretű programban való használathoz. Alapvető számítási ismeretek várhatók, de a vonatkozó matematikai információkat áttekintik. A programozás ismerete nem várható, de hasznos, mivel csak röviden ismertetem a programozás tényleges működését.
Amire szüksége lesz:
Személyi számítógép internet -hozzáféréssel
1. lépés: Az algoritmus megértése 1. rész: A határozott integrál és használata

Feltételezem, hogy egy kicsit tudja, mi az integrál az alapvető számítás összefüggésében. Az integrálok azért fontosak, mert lehetővé teszik az értékek tömbjének összegzését végtelen kicsi hosszúsággal megszorozva; ez hasznos a pénzügyek, számelmélet, fizika, kémia, valamint sok más területen. Ez a program azonban csak egy véges intervallumra teszi lehetővé a görbe alatti terület kiszámítását, vagy más szóval, nem értékeli az anti-derivátumokat-ehhez sokkal hatékonyabb algoritmus szükséges. Ez az algoritmus akkor hasznos, ha ki kell értékelnie egy meghatározott integrált egy nagyobb programban, valami más irányába, vagy ha ellenőrizni szeretné a válaszát, hogy nincs -e kézzel végzett meghatározott integrál.
Egy alapvető határozott integrál a függvény által meghatározott görbe alatti területet ábrázolja, pl. f (x). Egy határozott integrálhoz két pont (a és b jelzésű) közötti területet keressük. A képen a türkiz régió az a terület, amelyre utalok, és az ennek meghatározására szolgáló egyenlet is látható ebben a régióban. A képen látható funkció tetszőleges.
2. lépés: Az algoritmus megértése 2. rész: Numerikus közelítés

A számítógépnek széles körű utasításokra van szüksége, hogy kiszámítsa azt a területet egy tetszőleges függvény alatt, amely bármely funkcióhoz használható, így az Ön által jól ismert elemzési módszerek nem használhatók, mivel túlságosan specifikusak. Az integrálok hozzávetőleges kiszámításának egyik módja, amelyet egy számítógép ténylegesen képes kezelni, azáltal, hogy kitölti az érdeklődési területet a felhasználó által meghatározott mennyiségű egyenlő szélességű és változó magasságú téglalappal, majd összegzi a téglalap összes területét. A téglalapok merev tulajdonságai érintetlenül hagyják a teljes területet, ezért ezt közelítőnek tekintjük; azonban minél több téglalapot tud behúzni a határok (a és b) közé, annál pontosabb lesz a közelítés, mivel az érintetlen régiók ritkábbak lesznek. Mivel a számítógép elvégzi a feladatot, a kívánt régióban lévő téglalapok számát nagyon nagyra állíthatja, így a közelítés rendkívül pontos. A támogató képen képzelje el, hogy a kijelölt területen minden téglalap azonos szélességű. Mindent megtettem, hogy egyenlő szélességűek legyenek a Microsoft Paint alkalmazásban, de nem a legjobb munkát végeztem.
3. lépés: Az algoritmus megértése 3. rész: A középpont szabály

Ez a szabály határozza meg a téglalapok elkészítésének és felhasználásának módját. Az "N" téglalapok közül minden téglalapnak azonos szélességűnek kell lennie, Δx, de minden n -edik téglalap nem lehet teljesen azonos: a változó tényező a magasság, amely egy bizonyos ponton értékelt függvény szerint változik. A középpont szabály onnan kapta a nevét, hogy minden egyes téglalap magasságát f (x_n) -ként értékeli, ahol az "x_n" az egyes téglalapok középpontja, a téglalap bal vagy jobb oldalán. A középpont használata olyan, mint egy átlag megvalósítása, amely pontosabbá teszi a közelítést, mintha jobb vagy bal oldalt használná. Ennek a lépésnek az alátámasztó képe összefoglalja a középső pont matematikai meghatározásának módját.
4. lépés: A program létrehozása 1. rész: Python fordító/szerkesztő letöltése
Most, hogy megértette a végrehajtandó algoritmust, a számítógép elvégzése szükséges a számítás elvégzéséhez. Az első lépés ahhoz, hogy megmondja a számítógépnek, mit kell tennie, ehhez meg kell szereznie az eszközöket. Ez az algoritmus bármilyen nyelven kódolható; az egyszerűség kedvéért ez a program Python nyelven lesz kódolva. Ahhoz, hogy megparancsolja a számítógépnek, hogy végrehajtsa a műveleteket a Python segítségével, szüksége lesz egy szerkesztőre, amely az adott nyelven írt utasításokat fogadja el, majd lefordítja a számítógép által érthető gépi nyelvre, hogy elvégezhesse azokat a feladatokat, amelyeket Önnek meg kell tennie. Manapság a szerkesztő és a fordító rendszerint integrált, de ez nem mindig van így. Bármilyen szerkesztőt/fordítót használhat, amiben jól érzi magát, de megmutatom, hogyan szerezhetem meg személyes kedvencemet a Python: Canopy -hoz. Ha már rendelkezik szerkesztővel/fordítóval, kihagyhatja ezeket a lépéseket.
- Látogasson el a https://www.enthought.com/product/canopy/ oldalra
- Kattintson a Canopy letöltése lehetőségre
- Kattintson az operációs rendszerének megfelelő letöltés gombra
A letöltés automatikusan elindul
- Kövesse a telepítési utasításokat a végrehajtási fájl elindítása után
- Futtassa a Programot
- A program főmenüjében kattintson a "Szerkesztő" gombra
- A képernyő közepén kattintson az "új fájl létrehozása" gombra
Ettől kezdve egy üres fehér ablakot kell látnia, amelynek kurzora egy alapvető szövegszerkesztő dokumentumra hasonlít. Most már készen áll a határozott integrálok megoldására szolgáló numerikus integrációs algoritmus kódolására. Az eljárási lépések tartalmaznak egy kódrészletet, amelyet másolni fog, és magyarázatot ad arra, hogy ez a részlet mit tesz a program egészére.
5. lépés: A program létrehozása 2. rész: Funkciók importálása és változók meghatározása

Másolja a képen látható kódot.
Bármely program esetében, amelyik kódolást talál magának, lesznek változók. A változó egy olyan névnek adott név, amelyet működtetni fog, és amely változhat. A legtöbb programozási nyelvben (ha nem mindegyikben) inicializálni kell egy változót, mielőtt a program módosítani tudná. A program esetében a "N", "a" és "b" változókat neveztem el. Ezek az értékek reprezentálják az iterációk számát (AKA téglalapok száma), az alsó határt és a felső határt. Ezeket bármikor elnevezheti, de az "Az algoritmus megértése, 3. rész: A középponti szabály" című képletekhez illeszkedve a legjobb, ha változatlanul tartja őket. Vegye figyelembe, hogy nem csak egy adott értékre vannak beállítva. Ez azért van, mert olyan bemenetekről van szó, amelyek a program futtatásakor a program felhasználója meghatározhatják, hogy mi lesz az érték. Az idézőjelben lévő szöveg a bemeneti parancs után megjelenik a program futtatásakor, és megmondja, hogy milyen típusú értéket kell beírni. Azt is észre fogja venni, hogy az "int" és az "float" használatos a bemeneti jelölések előtt. Ezek a kifejezések megmondják a számítógépnek, hogy milyen típusú változó lesz ez az érték. Az "int" egész szám, az "float" pedig lebegőpontos érték (azaz tizedes). Világosnak kell lennie, hogy miért jelölik ezeket.
A "#" után megjelenő szöveg olyan megjegyzés, amely lehetővé teszi a programozó számára, hogy humanista módon kövesse a kódot; Bizonyos megjegyzéseket tettem a kódomban, amelyeket másolni fog, de nyugodtan adjon hozzá olyan megjegyzéseket, amelyek kifejezetten segítenek. A program nem fog semmit olvasni "#" karakterrel parancsként.
A kódnak az a része, amely "a matematikai importálástól *" olvasható, arra utasítja a programot, hogy importáljon egy sor matematikai függvényt, amelyek használhatók anélkül, hogy saját magukba kellene őket programozni. A "*" csak azt jelenti, hogy "minden". Olvassa el a kód ezen részét: a matematikai könyvtárból importálja az összes funkciót. Ez lehetővé teszi olyan matematikai függvények használatát, mint a szinusz, koszinusz, napló, exp, stb. Ezek a függvények matematikailag integrálhatók a kódba.
6. lépés: A program létrehozása 3. rész: Integrációs függvény létrehozása

Másolja a képen látható kódot az előző kód alá.
FIGYELMEZTETÉS: Ez a rész sűrű, és szeretnék tisztázni néhány olyan dolgot, amely zavaró lehet. Amikor a programozásról beszélünk, a "funkció" szó sokat felbukkan. Ez a kifejezés is sokat felbukkan, ha matematikáról beszél. Tehát innentől kezdve, amikor egy programozási értelemben vett funkcióról beszélek, a "Python függvény" -t fogom írni, és amikor a matematikai függvényről beszélek, akkor azt mondom, hogy "matematikai függvény". Egy bizonyos ponton a Python függvényt fogjuk használni a kérdéses matematikai függvény ábrázolásaként.
Ez a következő kódrészlet a program lényege. Itt definiálunk egy Python függvényt, amely a középpont szabály segítségével hajtja végre a numerikus integráció algoritmusát. "def Integrate (N, a, b)" így szól: definiálja az "Integrate" nevű függvényt, amely elfogadja az "N", "a" és "b" változókat, és visszaadja a görbe alatti területet (matematikai függvény) amely szintén az "Integrate" Python függvényen belül van definiálva. Ezt a Python -függvényt bármikor nevezheti a kódolás során, de érdemes integráltnak nevezni, mivel ez egy olyan funkció, amely valóban integrál egy matematikai függvényt.
Ezen a ponton érdemes megjegyzést fűzni ahhoz, hogy a Python hogyan különíti el a kódblokkokat. A kódblokk egy egész szakasz, amely egy bizonyos feladatot hajt végre. A különböző programozási nyelvek kijelölt módszerekkel megkülönböztetik ezeket a "blokkokat". A Python esetében egy blokkot behúzások különböztetnek meg: minden feladat-végrehajtó szakasznak saját behúzása van, és más behúzott blokkokon belül lehetnek behúzott blokkok. Ez a feladatokon belüli feladatokat jeleníti meg, és lényegében megmondja a kód végrehajtásának sorrendjét. A definiált "Integrate" Python függvény esetében a függvényen belül minden ki van zárva egy blokkból, így megkülönböztetve az adott funkción belül végrehajtandó feladatokat. A Python funkcióban vannak behúzott részek, amelyek saját feladataikat is ellátják. Ez a következőképpen történik: parancs (feladat) van megadva, kettőspont követi a parancsot, és amit a parancs végez, az alá van húzva.
Közvetlenül az "integrate" Python függvény definiálása után definiál egy másik Python függvényt, az f (x) nevet. Ez azt a matematikai függvényt jelenti, amelyet integrálni fognak. Minden egyes integrálni kívánt matematikai függvénynél ezt a programot kell végrehajtania, hogy megváltoztassa (ellentétben a program futtatásakor definiált változókkal). Minden Python függvénynek lesz visszatérési értéke, ezt adja vissza a függvény, amikor értéket dob. Ebben az esetben a bedobott érték "x", és ez az "x" kifejezés azt veszi figyelembe, amit valaha is dobott-ez egy ideiglenes érték.
Ezt követően egy for-ciklus az oktatóanyag "Az algoritmus megértése" szakaszának képleteiben meghatározott összegzésként működik. Ez az összegzés további pár változót igényel, amelyek közül az egyik a teljes "Integrate" Python függvény visszatérési értéke lesz. A for-loop előtt ezeket a változókat "értékként" és "érték2" -ként jelöltem ki. a for-loop feladata, hogy iteráljon egy kijelölt változó értéktartományán, amely kényelmesen meghatározható a for-loop parancsban; ebben az esetben ez a változó "n". Az iteráció tartománya 1 -től N+1 -ig terjed. Észre kell vennie, hogy a fent említett képletekben meghatározott összegzés csak 1 -től N -ig terjed. Ezt így határozzuk meg, mert a Python nyelv minden iterált értéket nullától kezdve számol, így lényegében át kell tolnunk az értékek tartományát, hogy megfeleljenek a kívántnak hatótávolság. A for-loop ezután lehetővé teszi a téglalap összes magasságának összegzését, és tárolja ezt az értéket az általam "értéknek" nevezett változóban. Ez látható a kódrészletben, amely így jelenik meg: érték += f (a +((n- (1/2))*((b-a)/N))).
Innentől kezdve a kód következő része az "value2" nevű változót használja, amelyet azután hozzárendelnek az egyes téglalapok magasságának összegéhez, szorozva az egyes téglalapok szabványos szélességével-ez a végső válaszunk programunk megjeleníti, és így az "Integrate" Python függvény visszatérési értéke.
7. lépés: A program létrehozása 4. rész: A válasz megjelenítése

Másolja a képen látható kódot az előző kód alá.
Most, hogy a választ az "Integrate" Python függvénnyel lehet megkapni, szeretnénk tudni megjeleníteni. Csak arról van szó, hogy a felhasználó által bevitt értékeket ("N", "a" és "b") az "Integrate" Python funkcióba helyezzük, és kinyomtatjuk a képernyőn. Ez a parancs a 21. sorban látható, és valójában csak annyit kell tennie, hogy befejezze ezt a lépést. A kód a 19. és 20. sorban csak azért van, hogy "szépítse" a teljes program kimenetét. A "print (" ………………………. ")" elválasztja a program bemeneti részét a kimeneti résztől, és a "print (" Itt a válasz: ")" csak egy megjelölés, amelyre a válasz a szöveg e sora után kell kinyomtatni.
8. lépés: A program futtatása 1. rész: A program futtatása úgy, ahogy van

Ha nem használja a Canopy -t, akkor valószínűleg egyáltalán nem kell követnie ezt a lépést, és a program futtatása eltérő eljárásokat igényelhet. A Canopy programban a program futtatása előtt el kell mentenie. A Python program fájltípusa.py fájl-automatikusan így menti. Válassza ki, hogy hová szeretné menteni a fájlt, majd futtathatja a programot.
A program futtatása:
- Nyomja meg a zöld gombot, amely úgy néz ki, mint egy "lejátszás gomb", amely az eszköztáron található, közvetlenül a fájlnév fölött (lásd a képet).
- A program ezután a szerkesztő alsó képernyőjén fut, amely a Canopy adatelemző környezet néven ismert. Ha feltételezzük, hogy az utasításokat másolta, ahogy írtam, akkor a Canopy adatelemző környezet alján a következő üzenetet kell látnia: "Adja meg, hogy hányszor szeretne összegezni (több alkalommal = pontosabban):." (lásd a képet)
- Adja meg azt az értéket, hogy hányszor szeretné megismételni az iterációt, azaz 10000 (hány téglalapot szeretne beilleszteni a területére), majd nyomja meg az enter billentyűt.
- További felszólítások jelennek meg olyan állításokkal, amelyek ismerős bemeneti utasítások, amelyeket az 5. lépésben kódolt a programba. Töltse ki megfelelően a fenti 3. szám szerint.
- Ki kell értékelni az integrált, és megjelenik az eredmény.
Ha a programot az előző képeken látható módon kódolta, akkor néhány határon belül integrálta az f (x) = x^2 programot. Az x^2 integrálját könnyen lehet kézzel értékelni, ezért ellenőrizze és győződjön meg arról, hogy a program nagyon közeli választ adott a kézzel meghatározott helyes analitikai értékre. Amikor a programot N = 10000, a = 0 és b = 10 értékkel futtatom, a 333.33333249999964 választ kapom. A helyes analitikai válasz a 333.333. Ez hihetetlenül pontos és gyors. Lényegében 10 000 téglalapot szorított 0 és 10 közé az x tengelyen, és ezekkel közelítette meg az x^2 görbe alatti területet!
9. lépés: A program futtatása 2. rész: Más matematikai függvények integrálása

Az előző lépésben, ha hűségesen követte, integrálta az f (x) = x^2 értéket. Nem ez az egyetlen matematikai függvény, amelyet a program integrálhat. Emlékezzen vissza az 5. lépésből, amikor importálta a programba a Python függvények matematikai könyvtár tömbjét. Ez lehetővé teszi bonyolultabb integrálható matematikai függvények használatát. Adjunk egyet. Természetesen tetszőleges funkciót használhat, de tovább mutatom ennek a kódnak a pontosságát azáltal, hogy integrálunk egy adott matematikai függvényt, amely egy bizonyos tartományba integrálva jól ismert értéket eredményez. Ez a függvény f (x) = Sin [x]. Ez a matematikai függvény jelenik meg az első kísérő képen, 0 és 2π között ábrázolva, és az érdeklődési terület türkiz árnyalatú. Ugyanannyi pozitív terület van, mint ebben az intervallumban negatív terület, tehát ha összeadja a teljes területet, akkor nullát kell kapnia. Nézzük meg, hogy ez valóban megtörténik -e:
Az f (x) = Sin [x] matematikai függvény beillesztése a programba:
- A program újbóli futtatása előtt a "#type your function after return" megjegyzésbe írja be: sin (x), ahol az x ** 2 jelenleg található. (lásd a képet).
- Futtassa a programot a zöld lejátszás gomb ismételt megnyomásával.
- Írja be az 10000 értéket az N értékhez (hányszor szeretné összegezni).
- írja be a "0" értéket az alsó határhoz.
- A felső határhoz (kb. 2π) írjon be 6.2832 értéket.
- Nézze meg, milyen értéket kap.
Amikor ezt megtettem, végül 1.079e-10 értéket kaptam: ez a.0000000001079 értéknek felel meg, ami valóban közel van a nullához, tehát pontosnak tűnik, és azt mutatja, hogy az algoritmus megfelelően kezeli a negatív területet.
10. lépés: A program futtatása 3. rész: A program kibővítése
Ezen a ponton készen áll: van egy működő, határozott integrált algoritmusa a Python -ban, amely zökkenőmentesen fut, és nagyon pontos válaszokat ad. Ez a program azonban javítható. Nem vagyok programozó, és minimális tapasztalattal rendelkezem a Pythonban. Valójában fel kellett frissítenem magam a Python használatával az oktatóanyag elvégzéséhez, de ez önbizalmat adhat Önnek abban, hogy a Python ilyen könnyen megtanulható nyelv. A lényeg az, hogy bővítheti ezt a programot azáltal, hogy hatékonyabbá teszi, esetleg megvalósít néhány GUI -t, és felhasználóbarátabbá teszi.
Gondolataim a program bővítéséről:
- Végezzen el egy grafikus felhasználói felületet, amely lehetővé teszi a program futtatását a Canopy interaktív adatelemző környezet használata nélkül
- Tegye úgy, hogy az integrálandó matematikai függvényt ne kelljen a program belsejébe bevinni, hanem a program futtatása után be lehet írni (kezdetben ezt próbáltam, de nem tudtam rájönni).
- Határozzon meg egy "Integrate" Python függvényt, hogy az f (x) függvényt úgy fogadja el, hogy az f (x) függvény benne legyen.
Ez csak néhány példa a fejlesztési területekre, de garantálom, hogy számos más területen is javítható. Így ezt a lépést példaként hagyom a program hibáira, és talán egy gyakorlatot annak, aki tovább akarja javítani a programot.
Ajánlott:
NAGY alfa-numerikus kijelző: 7 lépés (képekkel)

NAGY Alpha-numerikus KIJELZŐ: Kevés lehetőség van, ha olyan kijelzőre van szüksége, amely a szoba túloldalán látható, egy nagy kijelzőre. Készíthetsz olyat, mint az én "idő négyzet" vagy "led -ek üvegre", de ez körülbelül 40 óra unalmas munkát igényel. Tehát itt van egy egyszerű, hogy nagy kijelzőt készítsen. Az
Numerikus adatok küldése egyik Arduino -ból a másikba: 16 lépés
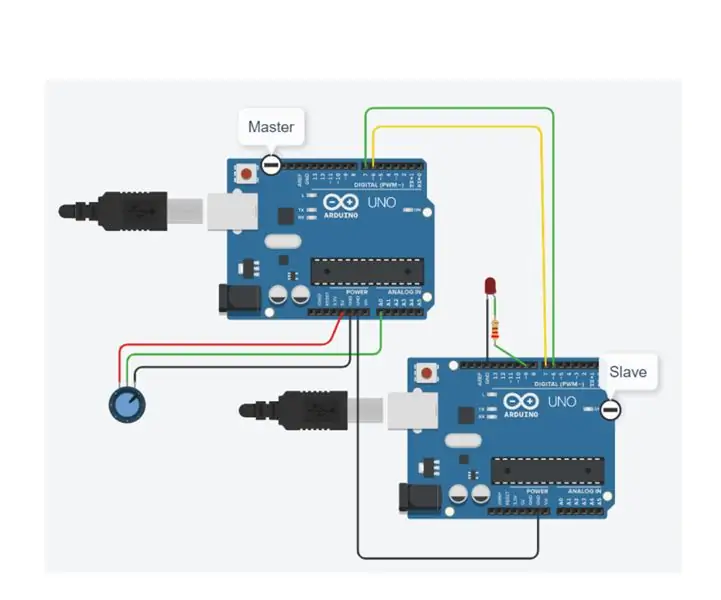
Numerikus adatok küldése egyik Arduino -ból a másikba: Bevezetés: David Palmer, CDIO Tech. az Aston Egyetemen. Volt valaha szükség néhány szám küldésére az egyik Arduino -ról a másikra? Ez az utasítás megmutatja, hogyan. Könnyen kipróbálhatja működését, ha egyszerűen beír egy számsort, amelyet el kell küldeni az S
Integrációs platform Ubidots LOGO -val! Siemens a Node-RED használatával: 13 lépés

Integrációs platform Ubidots LOGO -val! Siemens a Node-RED használatával: ap Néhány hétig néhány tesztet végeztem LOGO-val! (logikai modul) a Siemens -től, néhány hónapja láttam, hogy alapvető ipari alkalmazásokban használják, bár személy szerint nem tartom 100% -ban PLC -nek, könnyen integrálható a mon
Hogyan lehet kiszámítani a trapéz területét Pythonban?: 5 lépés
Hogyan lehet kiszámítani egy trapéz területét Pythonban?: Ezzel az utasítással a python program segítségével megismerheti az adott trapéz területét
Hogyan készítsünk nagyszülők naptárát & Scrapbook (még akkor is, ha nem tudja, hogyan kell a Scrapbookot írni): 8 lépés (képekkel)

Hogyan készítsünk nagyszülők naptárát & Scrapbook (még ha nem is tudod, hogyan kell a Scrapbookot írni): Ez egy nagyon gazdaságos (és nagyra értékelt!) Ünnepi ajándék a nagyszülőknek. Idén 5 naptárat készítettem, egyenként kevesebb mint 7 dollárért. Anyagok: 12 nagyszerű fotó gyermekéről, gyermekeiről, unokahúgairól, unokaöccseiről, kutyáiról, macskáiról vagy más rokonairól12 különböző darab
