Alapvető 3D szkenner a digitális 3D leképezéshez: 5 lépés

2024 Szerző: John Day | [email protected]. Utoljára módosítva: 2024-01-30 09:40

Ebben a projektben leírom és elmagyarázom a 3D szkennelés és rekonstrukció alapvető alapjait, amelyeket elsősorban a kis félsíkú tárgyak szkennelésére alkalmaznak, és amelyek működése kiterjeszthető a távvezérlő repülőgépekre telepíthető szkennelési és rekonstrukciós rendszerekre is. egy 3D modell. azokról a helyekről, ahol az őket szállító repülőgép repül

A végső ötlet az, hogy 3D -s beolvasást végezzünk egy helyről vagy területről, akár külső, akár belső térről, hogy digitális térképként használjuk (mint a Prometeus filmjében)

1. lépés:

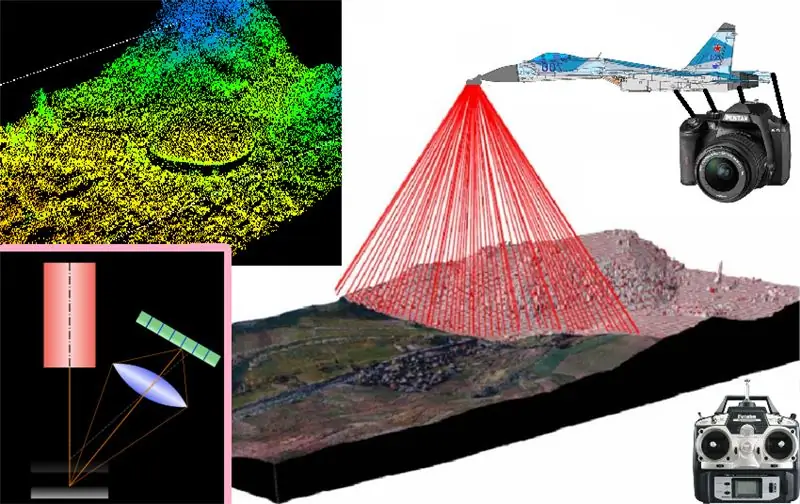
az ötlet az, hogy a teljes 3D szkennelési rendszert egy távirányítású síkra kell telepíteni, annak érdekében, hogy digitalizáljuk minden olyan terület virtuális térképét, amelyen 3D-ben repül, de ehhez a lézeres háromszögelés működésének elejétől kezdtük A szkennelés vagy a 3D rekonstrukció lézeres háromszögeléssel alapvetően abból áll, hogy egy lézersugarat egy prizmán keresztül vezetünk, amely lézercsíkot generál, hogy egy teljes lézersávot kapjunk, amelyet a szkennelni kívánt tárgyra vetítenek, és miután ezt a lézer vetületet a felületi felület A beolvasás helyéről a képet valamilyen kamerával kell rögzíteni, és lehetőleg ismerni kell a kibocsátott lézersáv kivetítési szögéhez viszonyított szöget, mivel ezek a képek mindegyike rögzíti a vetített lézersávokat. Az objektum felületén előfeldolgozásra kerülnek, hogy kinyerjék a beolvasandó objektum méretjellemzőit, és egyszerűen szalagról szalagra szkenneljenek az objektum felett, hogy megkapják a felület profilját az objektum ezen keresztirányú szegmensében, majd rögzítsék az objektum következő keresztmetszetének kivetített csíkja, hogy az összes vetített csíkot összeadja az obto összes keresztmetszete előtt megkapjuk a felületének háromdimenziós letapogatását

2. lépés:

Mivel azonosítottuk célkitűzéseinket, a következő lépés annak tudatában, hogy a felszálláshoz először szilárdan a talajon kell lennie, ezért a földön egy lineáris 3D szkenner kísérleti prototípusával kezdtük az alap működését. 3D -s szkennelés és ahogy a fenti képen is látható, PC -t, OpenCV -t, OpenLL Glutet, webkamerát, lézert, lézerfarm -generátort (jelen esetben forgótükörön keresztül), elektronikus lineáris elmozdító rendszert használtam (sínnel és egy régi nyomtatóból kivont rendszer) egy alapból, amelyre a beolvasandó tárgyakat, fát és gyurmát helyezem, és amint a fotón is látható, a számítógépen: sikerült Glutinnal generálnom és megjelenítenem az OpenGL-ből egy három- dimenziós modell, amelyet a beolvasott valós tárgy (jelen esetben egy játékpók) alapján reprodukálnak

így több mint nyilvánvaló, hogy a működési elv működőképes, és hogy a megfelelő beállításokkal és a repülő rendszerhez való alkalmazkodással képes lesz beolvasni és reprodukálni a repülési terület 3D térképét.

De ez a rendszer csak arra szolgál, hogy 3D térképeket nyerjen azokról a helyekről, amelyeken átrepül ???

3. lépés:

a barlangok és csatornák belsejének feltérképezése (csakúgy, mint a Prometeus filmben) Ez a 3D-s szkennelési rendszer a nagy és üreges tárgyak, például barlangok, épületek, alagutak stb. belsejének háromdimenziós modelljeinek rekonstruálására is szolgál. működési elve pontosan ugyanaz, mint a már leírtak, és alapvetően a következőkből áll:

1. rögzítse a fényképet a lézersáv minden vetítéséről a beolvasandó felületen
2. szűrje le és távolítsa el a színt a képről
3. binarizálja a színt dinamikus képküszöbbel
4. Élészlelőt kell alkalmazni, hogy felismerje az egyes lézeres vetületek keresztmetszetének rögzített profilját
5. és a szegmentálás segítségével válassza ki a megfelelő szegélyt a beolvasni és rekonstruálni kívánt objektum keresztmetszetének 3D -s ábrázolásához a virtuális 3D térképen
6. akkor ezeket a lépéseket egyszerűen meg kell ismételni minden egyes fényképen, amelyet az egyes alszakaszok alszakaszai által folyamatosan kivetített lézersávokról készítenek.

a keresztmetszetek ábrázolásának rétegről rétegre történő hozzáadása egymás után történik, amíg egy pontfelhőt nem kapunk, amelyet a leképezni kívánt objektum keresztmetszeteinek számos ábrázolása alkot

4. lépés:

Ezután átadom a felszíni lézersávok vetületeinek képfeldolgozására szolgáló programokat. és ezeknek a szusszív transzverzális ábrázolásoknak a virtuális 3D rekonstrukciójáról a kidolgozott háromdimenziós térképmodellben:

képfeldolgozás:

n

#include #include "cv.h" #include "highgui.h" #include // #include #include #include #include

char f = 0; char név = {"0.jpg"}; int n = 0, s, x, y; CvScalar sp; FÁJL *NuPu;

void Writepoints () {char bufferx [33], buffery [33]; itoa (x, bufferx, 10); itoa (y, puffer, 10); fprintf (NuPu, bufferx); fprintf (NuPu, "\ t"); fprintf (NuPu, buffery); fprintf (NuPu, "\ n"); }

void noteblockInit () {NuPu = fopen ("NuPu.txt", "w"); fseek (NuPu, 0, 0); fprintf (NuPu, "NP:"); fprintf (NuPu, "\ n"); }

int main () {char argstr [128]; noteblockInit (); cout << "Teklea!…:" f; név [0] = f; cout <

IplImage* img0 = cvLoadImage ("00.jpg", 0); if (f == '0') {for (y = 1; yheight-2; y ++) {for (x = 1; xwidth-2; x ++) {sp = cvGet2D (img0, y, x); if (sp.val [0]> 50) {Writepoints (); n ++;}}}} else {for (y = 1; yheight-2; y ++) {for (x = 1; xwidth-2; x ++) { sp = cvGet2D (img1, y, x); if (sp.val [0]> 50) {Writepoints (); n ++;}}}} char buffer [33]; itoa (n, puffer, 10); fprintf (NuPu, "Fin:"); fprintf (NuPu, puffer); fprintf (NuPu, "\ n"); fclose (NuPu);

cvWaitKey (0); //_execlp("calc.exe "," calc.exe ", argstr, NULL); cvDestroyAllWindows (); cvReleaseImage (& kép); cvReleaseImage (& img); cvReleaseImage (& img0); cvReleaseImage (& img1); cvReleaseImage (& img2); visszatérés 0; }

3D rekonstrukció:

#include //////////////////ifdef _APPLE_ #include #else #include #include #endif #include #include #include #include #include #include

#define violeta glColor3f (1, 0, 1) #define azul glColor3f (0, 0, 1) #define turkeza glColor3f (0, 1, 1) #define verde glColor3f (0, 1, 0) #define amarillo glColor3f (1, 1, 0) #define naranja glColor3f (1,.3, 0) #define rojo glColor3f (1, 0, 0) névtér használatával std; int s, Boton = 1, Pulbut = 1; float mx = 0, my = 0, mtx = 0, mty = 0, mtz = -5,0; const int Avance = 1; karakterlánc, Aux; char Karakter = 'H'; FÁJL *NuPu; int NP, h, w; float G = 0, n = 0, cx [5000], cy [5000], x, y, ax, ay, az; int betűtípus = (int) GLUT_BITMAP_8_BY_13; statikus char címke [100]; szénpuffer [3]; GLfloat anguloCuboX = 0.0f; GLfloat anguloCuboY = 0.0f; GLfloat anguloEsfera = 0.0f; GLint horgony = 500; GLint alto = 500; int hazPerspectiva = 0; void reshape (int szélesség, int magasság) {glViewport (0, 0, szélesség, magasság); glMatrixMode (GL_PROJECTION); glLoadIdentity (); if (hazPerspectiva) gluPerspective (23.0f, (GLfloat) szélesség/(GLfloat) magasság, 1.0f, 20.0f); más glOrtho (-1, 1, -1, 1, -10, 10); glMatrixMode (GL_MODELVIEW); ancho = szélesség; alto = magasság; } void Kolorear (int K) {float Hip; x = (cx [s] -320)/480; y = (cy [s] -240)/640; Csípő = sqrt (pow (x, 2)+pow (y, 2)); ha ((csípő> = 0) && (csípő =.07) && (csípő =.14) && (csípő =.21) && (csípő =.28) && (csípő =.35) && (csípő =.42) && (Csípő <=. 49)) {violeta;}} void drawNuPu (void) {glColor3f (1, 1, 1); glBegin (GL_LINES); glVertex3f (.2, 0, 0); glVertex3f (-.2, 0, 0); glVertex3f (0,.2, 0); glVertex3f (0, -2, 0); glEnd (); rojo; glBegin (GL_POINTS); for (n = 0; n <10; n ++) {for (s = 0; s void setOrthographicProjection () {glMatrixMode (GL_PROJECTION); glPushMatrix (); glLoadIdentity (); gluOrtho2D (0, w, 0, h); glScalef (1, -1, 1); glTranslatef (0, -h, 0); glMatrixMode (GL_MODELVIEW);} void renderBitmapString (float x, float y, void *font, char *string) {char *c; glRasterPos2f (x, y); for (c = string; *c! = '\ 0'; c ++) {glutBitmapCharacter (font, *c);}} void display () {// mx = 468; itoa (mx, puffer, 10); glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // glLoadIdentity (); glColor3f (1.0, 1.0, 1.0); glRasterPos2f (-1,.9); // glutBitmapString (GLUT_BITMAP_SIM_SIM;; s <3; s ++) {glutBitmapCharacter (GLUT_BITMAP_TIMES_ROMAN_24, buffer [s]);} glTranslatef (mty, -mtx, mtz); glRotatef (mx, 1.0f, 0.0f, 0.0f); glRotatef (my, 0.0f, 1.0f, 0.0f); drawNuPu (); /*glColor3f(1.0, 1.0, 1.0); glRasterPos2f (.5,.5); // glutBitmapString (GLUT_BITMAP_TIMES_ROMAN_24, "Hello Text"); glutBitmapCharacterAP (GLU_BIM_));* / /*glColor3f (1. 0f, 1,0f, 1,0f); setOrthographicProjection (); glPushMatrix (); glLoadIdentity (); renderBitmapString (30, 15, (void *) betűtípus, "GLUT Tutorial ---_ ------ _@ 3D Tech"); */ glFlush (); glutSwapBuffers (); anguloCuboX+= 0,1f; anguloCuboY+= 0,1f; anguloEsfera+= 0,2f; } void init () {glClearColor (0, 0, 0, 0); glEnable (GL_DEPTH_TEST); ancho = 500; alt=500; } void leer () {ifstream myfile ("A:/Respaldo 2016. szeptember/D/Respaldos/Respaldo compu CICATA abril 2015/usb1/rekostruccion 3D en Especialidad CICATA/Software/Reconstruccion 3D/R3d_0 / bin/Debug/NuPu.txt"); if (myfile.is_open ()) {s = 0; while (getline (myfile, line)) {if (([0] sor! = 'N') && ([0] sor! = 'F')) {Aux = sor; [0] sor = 48; sor [1] = 48; sor [2] = 48; sor [3] = 48; cy [s] = atoi (line.c_str ()); Aux [4] = 48; Aux [5] = 48; Aux [6] = 48; // Aux [7] = 48; cx [s] = atoi (Aux.c_str ()); s ++; }} myfile.close (); } else cout <1780) NP = 1700; cout <void idle () {display (); } üres billentyűzet (előjel nélküli char billentyű, int x, int y) {switch (key) {case 'p': case 'P': hazPerspectiva = 1; átalakítani (ancho, alt); szünet; „o” eset: „O” eset: hazPerspectiva = 0; átalakítani (ancho, alt); szünet; 27. eset: // menekülési kijárat (0); szünet; }} void raton (int gomb, int állapot, int x, int y) { / * GLUT_LEFT_BUTTON 0 GLUT_MIDDLE_BUTTON 1 GLUT_RIGHT_BUTTON 2 GLUT_DOWN 0 GLUT_UP 1 * / Boton = gomb; Pulbut = állapot; // mx = y; kijelző(); } void ratmov (int x, int y) {if ((Boton == 0) & (Pulbut == 0)) {mx = y; az én = x; } ha ((Boton == 2) & (Pulbut == 0)) {mtx = (y/200) -1; mty = (x/200) -1; } ha ((Boton == 1) & (Pulbut == 0)) {mtz =-(y/40) -5; } display (); } int main (int argc, char ** argv) { /*glutAddMenuEntry () glutAddSubMenu () glutAttachMenu () glutCreateMenu () glutSetMenu () glutStrokeCharacter () glutStrokeLength ()* / /*gl frame buffer glGetPixelMapfv () a megadott pixeltérkép visszaadása glGetPixelMapuiv () a megadott pixeltérkép visszaadása glGetPointerv () A megadott mutató címét adja vissza.*/ Init (); rábámul(); glutInit (& argc, argv); glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB); glutInitWindowPosition (50, 50); glutInitWindowSize (ancho, alt); glutCreateWindow ("Cubo 1"); benne(); glutDisplayFunc (kijelző); glutReshapeFunc (átalakítás); glutIdleFunc (tétlen); glutMouseFunc (raton); glutMotionFunc (ratmov); glutKeyboardFunc (billentyűzet); glutMainLoop (); visszatérés 0; }

5. lépés:

pillanatra abba kell hagynom! … De a következő fejezetben megígérem, hogy megvalósítom a málna pi 3-on vagy a jetson nanolapomon, amelyet már távirányítású repülőgépre szereltem, vagy valami pókrobotra, hogy átvizsgálja a barlangok belsejét