
Tartalomjegyzék:
- Szerző John Day [email protected].
- Public 2024-01-30 09:43.
- Utoljára módosítva 2025-01-23 14:48.

Az utóbbi időben sok munka történt az objektumok önkiegyenlítésében. Az önegyensúlyozás fogalma a fordított inga kiegyensúlyozásával kezdődött. Ez a koncepció kiterjedt a repülőgépek tervezésére is. Ebben a projektben a PID (arányos, integrált, származtatott) algoritmus segítségével egy kis önmérlegű robot modellt terveztünk. Azóta ez a módszer az ipari folyamatvezérlő rendszerek új arca. Ez a jelentés áttekinti az objektumok önegyensúlyozásának módszereit. Ezt a projektet féléves projektként hajtottuk végre, hogy megértsük a PID összefüggését a különböző ipari folyamatok hatékonyságával. Itt csak arra összpontosítunk, hogy rövid áttekintést nyújtsunk a PID -szabályozás hatékonyságáról és alkalmazásáról. Ezt a dokumentumot azáltal hozták létre, hogy röviden bemutatják a vezérlőrendszereket és a kapcsolódó terminológiákat, kiegészítve a projekt motivációival. Kísérleteket és megfigyeléseket végeztünk, érdemeket és hátrányokat írtunk le, és a jövőbeli fejlesztéseknél véget értek. Az önkiegyenlítő robot modelljét azért fejlesztették ki, hogy megértsék a PID hatékonyságát a vezérlőrendszer világában. Néhány szigorú teszten és kísérleten keresztül felfedezték a PID szabályozó rendszer előnyeit és hátrányait. Kiderült, hogy a PID -szabályozás számos előnye ellenére a korábbi módszerekhez képest ez a rendszer még sok fejlesztést igényel. Remélhetőleg az olvasó jól megérti az önkiegyenlítés fontosságát, a PID -szabályozás hatékonyságát és hiányosságait.
1. lépés: Bevezetés
A számítógépek megjelenésével és a folyamatok iparosodásával az emberiség történelme során mindig is folytak kutatások a folyamatok újbóli meghatározására és ami még fontosabb, azok önálló vezérlésére. A cél az, hogy csökkentsük az emberek részvételét ezekben a folyamatokban, ezáltal csökkentve a hibákat ezekben a folyamatokban. Ezért fejlesztették ki a „Vezérlőrendszer -tervezés” területét. A vezérlőrendszer -tervezést úgy lehet meghatározni, hogy különböző módszereket használnak egy folyamat működésének ellenőrzésére vagy állandó és előnyben részesített környezet karbantartására, legyen az kézi vagy automatikus.
Egy egyszerű példa lehet a helyiség hőmérsékletének szabályozása. A kézi vezérlés azt jelenti, hogy egy személy jelen van a helyszínen, aki ellenőrzi a jelenlegi körülményeket (érzékelő), összehasonlítja azt a kívánt értékkel (feldolgozás), és megteszi a megfelelő lépéseket a kívánt érték elérése érdekében (működtető). A probléma ezzel a módszerrel az, hogy nem túl megbízható, mivel egy személy hajlamos hibákra vagy hanyagságra a munkájában. Ezenkívül egy másik probléma az, hogy a hajtómű által elindított folyamat sebessége nem mindig egyenletes, vagyis néha előfordulhat, hogy gyorsabban, mint szükséges, vagy néha lassú. A probléma megoldása az volt, hogy mikrovezérlőt használtak a rendszer vezérlésére. A mikrovezérlő az
programozva a folyamat vezérlésére, adott specifikációk szerint, egy áramkörbe kapcsolva (később tárgyaljuk), betáplálva a kívánt értéket vagy körülményeket, és ezáltal vezérli a folyamatot a kívánt érték fenntartása érdekében. Ennek a folyamatnak az az előnye, hogy nincs szükség emberi beavatkozásra. Ezenkívül a folyamat sebessége egyenletes
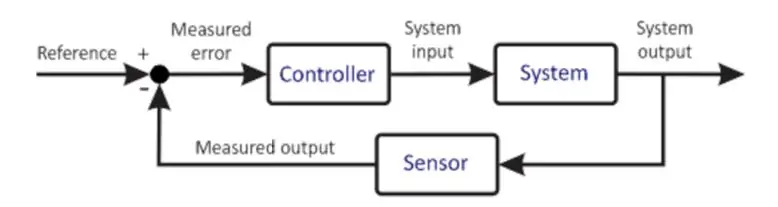
Alapvető vezérlőrendszer
Az előző diagram egy vezérlőrendszer nagyon leegyszerűsített változatát mutatja. A mikrokontroller minden vezérlőrendszer középpontjában áll. Ez egy nagyon fontos összetevő, ezért a kiválasztását gondosan kell elvégezni a rendszer követelményei alapján. A mikrovezérlő bemenetet kap a felhasználótól. Ez a bemenet határozza meg a rendszer kívánt állapotát. A mikrovezérlő visszajelzést is kap az érzékelőtől. Ez az érzékelő a rendszer kimenetéhez van csatlakoztatva, amelynek információit visszajuttatja a bemenetre. A mikroprocesszor programozása alapján különféle számításokat végez, és kimenetet ad a hajtóműnek. A hajtómű a kimenet alapján vezérli az üzemet, hogy megpróbálja fenntartani ezeket a feltételeket. Példa lehet egy motorvezető, aki olyan motort hajt, ahol a motor meghajtója a hajtómű, a motor pedig az üzem. A motor tehát adott sebességgel forog. A csatlakoztatott érzékelő leolvassa az üzem jelenlegi állapotát, és visszaadja azt a mikrovezérlőnek. A mikrovezérlő ismét összehasonlítja, számításokat végez, és így a ciklus megismétlődik. Ez a folyamat ismétlődő és végtelen, így a mikrovezérlő fenntartja a kívánt feltételeket
2. lépés: PID -alapú vezérlőrendszer
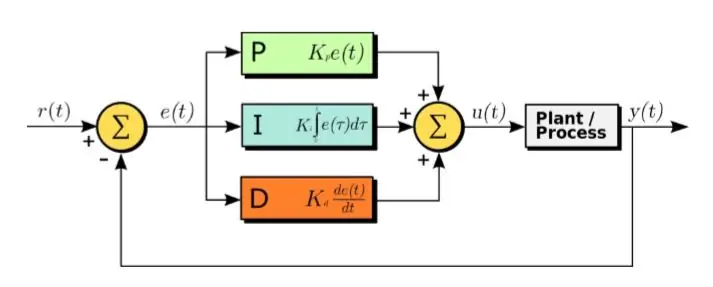

A PID algoritmus egy hatékony módszer a vezérlőrendszer tervezésére.
Meghatározás
A PID jelentése arányos, integrált és származtatott. Ebben az algoritmusban a kapott hibajel a bemenet. És a következő egyenletet alkalmazzuk a hibajelre
U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integrál (e (t)) (1.1)
Rövid magyarázat
Amint az a fenti egyenletből látható, a hibajelek integrálját és deriváltját kiszámítjuk, megszorozzuk a megfelelő állandókkal, és hozzáadjuk az e (t) -el megszorozott Kp állandóhoz. A kimenet ezután a hajtóműbe kerül, amely a rendszert működteti. Most nézzük sorban a funkció minden részét. Ez a funkció közvetlenül befolyásolja az emelkedési időt, az esési időt, a csúcsidőt, a leülepedési időt és az egyensúlyi állapot hibáját.
• Arányos rész: Az arányos rész csökkenti az emelkedési időt és csökkenti az egyensúlyi állapot hibáját. Ez azt jelenti, hogy a rendszer kevesebb időt vesz igénybe a csúcsérték eléréséhez, és amikor eléri az egyensúlyi állapotot, az egyensúlyi állapot hibája alacsony lesz. Ez azonban növeli a csúcs túllépést.
• Származékos rész: A származtatott rész csökkenti a túllépést és a letelepedési időt. Ez azt jelenti, hogy a rendszer átmeneti állapota jobban csillapodik. Ezenkívül a rendszer rövidebb idő alatt eléri az állandósult állapotát. Ennek azonban nincs hatása az emelkedési időre vagy az egyensúlyi állapot hibájára.
• Integrált rész: Az integrált rész csökkenti az emelkedési időt és teljesen kiküszöböli az egyensúlyi állapot hibáját. Ez azonban növeli a csúcs túllépést és az ülepedési időt.
• Hangolás: Egy jó vezérlőrendszer alacsony emelkedési idővel, ülepedési idővel, csúcs túllépéssel és egyensúlyi hibával rendelkezik. Ezért a Kp -t, Kd -t, Ki -t véglegesen be kell állítani, hogy a fenti tényezők hozzájárulását kiigazítsák egy jó vezérlőrendszer megszerzése érdekében.
A mellékelt ábra a PID algoritmus különböző paramétereinek megváltoztatásának hatását mutatja be.
3. lépés: Önegyensúlyozó robot

Az önegyensúlyozó robot többrétegű, kétkerekű robot.
A robot megpróbálja kiegyensúlyozni magát, ha bármilyen egyenlőtlen erőt alkalmaz. Egyensúlyba hozza magát a robotra ható erők hatására fellépő erő alkalmazásával.
Az önegyensúlyozás módszerei
Négy módszer létezik a robotok kiegyensúlyozására. Ezek a következők:
Önegyensúlyozás két infravörös dőlésérzékelő segítségével
Ez az egyik legdurvább módja a robot kiegyensúlyozásának, mivel nagyon kevesebb hardvert és viszonylag egyszerű algoritmust igényel. Ebben a megközelítésben két döntött IR érzékelőt használnak a talaj és a robot közötti távolság mérésére. A kiszámított távolság alapján a PID használható a motorok meghajtására, hogy ennek megfelelően kiegyenlítse a robotot. Ennek a módszernek az egyik hátránya, hogy az infravörös érzékelő kihagyhat néhány leolvasást. Egy másik probléma az, hogy megszakítás és hurkok szükségesek a távolság kiszámításához, ami növeli az algoritmus időbeli összetettségét. Ezért ez a robot kiegyensúlyozási módszer nem túl hatékony.
Önegyensúlyozás gyorsulásmérő segítségével
A gyorsulásmérő a test gyorsulását adja meg 3 tengelyen. Az y tengelyen (felfelé) és az x tengelyen (előre) orientált gyorsulás megadja a mértéket a gravitációs irány kiszámításához, és így a dőlésszög kiszámításához. A szöget a következőképpen kell kiszámítani:
θ = arktán (Ay/Axe) (1.2)
Ennek a módszernek az a hátránya, hogy a robot mozgása során a vízszintes gyorsulás is hozzáadódik az értékekhez, ami nagyfrekvenciás zaj. Ezért a dőlésszög pontatlan lesz.
Önegyensúlyozás giroszkóppal
Giroszkóppal kiszámítják a három tengely mentén az angluáris sebességeket. A dőlésszöget a következő egyenlettel kapjuk meg.
θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)
A giroszkóp használatának egyik nagy hátránya, hogy kicsi egyenáramú torzítással rendelkezik, ami alacsony frekvenciájú zaj, és néhány idő múlva a visszaadott értékek teljesen rosszak. Ez az integráció után a nulla pont eltávolodását eredményezi. Ennek eredményeképpen a robot egy ideig függőleges helyzetben marad, és a sodródás után felborul.
Önegyensúlyozás gyorsulásmérő és giroszkóp segítségével
Amint azt fentebb tárgyaltuk, csak gyorsulásmérő vagy giroszkóp használata nem adja meg a helyes dőlésszöget. Ennek érdekében gyorsulásmérőt és giroszkópot is használnak. Mindkettő be van ágyazva az MPU6050 -be. Ebben megkapjuk mindkettőjük adatait, majd összeolvasztjuk őket Kalman -szűrő vagy kiegészítő szűrő használatával.
• Kalman -szűrő: A Kalman -szűrő a zajos mérésekből kiszámítja a dinamikus rendszer állapotának legjobb becslését, minimálisra csökkentve a becslés négyzetes hibáját. A rendszer dinamikáját leíró diszkrét sztochasztikus egyenletek alapján két szakaszban, előrejelzésben és korrekcióban működik. Ez azonban nagyon összetett algoritmus, különösen egy mikrokontroller korlátozott hardverén.
• Kiegészítő szűrő: Ez az algoritmus elsősorban a giroszkópból nyert adatokat használja, és idővel integrálja a dőlésszög meghatározásához. A gyorsulásmérő leolvasásainak egy kis részét is használja. A kiegészítő szűrő valójában minimalizálja a gyorsulásmérő nagyfrekvenciás zaját és a giroszkóp alacsony frekvenciájú zaját, majd összeolvasztja őket, hogy a legjobb pontos dőlésszöget biztosítsa.
4. lépés: A robot tervezése
Önarányos robotot terveztünk az MPU6050 kiegészítő szűrő által megvalósított arányos származtatott vezérlő használatával. Az önkiegyenlítő robot kis modellje bemutatja nekünk a vezérlőrendszerek hasznosságát a robotok önkiegyenlítésében.
Rendszer implementáció:
A rendszer önkiegyenlítő robot. Ezt a PID vezérlővel hajtják végre, amely egy arányos integrált származékos vezérlő. Egyensúlyba hozzuk a robotot, ha kerekeit az esés irányába hajtjuk. Ennek során megpróbáljuk a robot súlypontját a forgáspont fölött tartani. Ahhoz, hogy a kerekeket az esés irányába vezesse, tudnunk kell, hol esik a robot, és milyen sebességgel esik. Ezeket az adatokat az MPU6050 segítségével nyerik, amely gyorsulásmérővel és giroszkóppal rendelkezik. Az MPU6050 méri a dőlésszöget, és a kimenetet átadja a mikrovezérlőnek. Az MPU6050 az I2C -n keresztül kapcsolódik az STM táblához. Az I2C -ben egy vezeték az óra számára, amelyet SCL -nek neveznek. A másik az adatátvitelre szolgál, amely SDA. Ebben a master slave kommunikációt használják. A kezdőcímet és a befejező címet úgy határozták meg, hogy tudják, honnan indulnak és hol végződnek az adatok. Itt implementáltuk a kiegészítő szűrőt az MPU6050 számára, amely egy matematikai szűrő a gyorsulásmérő és a giroszkóp kimeneteinek egyesítésére. Az adatok beszerzése után az MPU6050 -ből a mikrokontroller számításokat végez, hogy megtudja, hol esik. A számítások alapján az STM mikrovezérlő parancsokat ad a motorvezetőnek, hogy vezesse a járműveket az esés irányába, ami kiegyensúlyozza a robotot.
5. lépés: A projekt összetevői



A következő komponenseket használták az önkiegyenlítő robot projektben:
STM32F407
Az ST Microelectronics által tervezett mikrovezérlő. Működik az ARM Cortex-M architektúrán.
Motorhajtó L298N
Ez az IC a motor működtetésére szolgál. Két külső bemenetet kap. Az egyik a PWM jelet szolgáltató mikrokontrollerből. Az impulzus szélességének beállításával a motor fordulatszáma állítható. Második bemenete a motor meghajtásához szükséges feszültségforrás, ami esetünkben 12V -os akkumulátor.
DC motor
Az egyenáramú motor egyenáramú tápegységről működik. Ebben a kísérletben az egyenáramú motor a motorvezérlőhöz csatlakoztatott optocsatolók segítségével fut. A motor meghajtásához az L298N motorhajtást használtuk.
MPU6050
Az MPU6050 segítségével információt szerezhet arról, hogy hol esik le a robot. Méri a dőlésszöget a nulla dőlésponthoz képest, amely az MPU6050 helyzete, amikor a program futni kezd.
Az MPU6050 3 tengelyes gyorsulásmérővel és 3 tengelyes giroszkóppal rendelkezik. A gyorsulásmérő a három tengely mentén méri a gyorsulást, a giroszkóp pedig a három tengely körüli szögsebességet. A kimenet kombinálásához ki kell szűrnünk mindkettő zaját. A zajok kiszűréséhez van Kalman és kiegészítő szűrő. Kiegészítő szűrőt dolgoztunk ki projektünkben.
Opto pár 4N35
Az optocsatoló az áramkör kisfeszültségű és nagyfeszültségű részének elkülönítésére használt eszköz. Ahogy a neve is sugallja, fény alapján működik. Amikor az alacsony feszültségű rész jelet kap, áram folyik a nagyfeszültségű részben
6. lépés: A robot felépítése
A robot szerkezete a következőképpen magyarázható:
Fizikai szerkezet
Az önkiegyenlítő robot két rétegből áll, amelyek átlátszó műanyag üvegből állnak. Két réteg részleteit az alábbiakban adjuk meg:
Első réteg
Az első réteg alsó részébe egy cellát helyeztünk az STM tábla táplálására. Mindkét oldalon két, egyenként 4 voltos motort helyeztek el, amelyekhez a robot mozgatásához gumiabroncsok vannak csatlakoztatva. Az első réteg felső részében két egyenként 4 voltos elem (összesen 8 volt) és a motorvezérlő IC (L298N) van elhelyezve a motorok működtetéséhez.
Második réteg
A robot felső rétegében az STM táblát a Perf Boardra helyeztük. Egy másik, 4 optocsatolóból álló perf deszkát helyezünk a felső rétegre. A giroszkópot a robot felső rétegére is helyezik az alsó oldalról. Mindkét alkatrészt a középső részbe helyezzük, hogy a súlypont a lehető legalacsonyabb szinten maradjon.
Robot súlypontja
A súlypont a lehető legalacsonyabb szinten marad. Ebből a célból nehéz elemeket helyeztünk az alsó rétegre, könnyű elemeket, például STM kártyát és optocsatolókat a felső rétegre.
7. lépés: Kód
A kódot az Atollic TrueStudio segítségével állítottuk össze. Az STM stúdiót hibakeresési célokra használták.
8. lépés: Következtetés
Sok kísérletezés és megfigyelés után végül arra a pontra jutunk, ahol összefoglaljuk eredményeinket, és megbeszéljük, hogy milyen mértékben sikerült megvalósítani és kidolgozni a rendszer hatékonyságát.
Általános áttekintés
A kísérlet során a motor fordulatszámát sikeresen ellenőrizték a PID algoritmus segítségével. A görbe azonban nem éppen sima egyenes. Ennek számos oka lehet:
• Bár az érzékelő aluláteresztő szűrőhöz van csatlakoztatva, továbbra is bizonyos végleges kikapcsolásokat biztosít; ezek a nemlineáris ellenállásoknak és az analóg elektronika néhány elkerülhetetlen okának köszönhetők.
• A motor nem forog simán kis feszültség vagy PWM alatt. Olyan rángatásokat biztosít, amelyek hibás értékeket okozhatnak a rendszerben.
• A lengés miatt az érzékelő hiányozhat néhány réstől, amelyek magasabb értékeket biztosítanak. • A hibák másik fő oka az STM mikrovezérlő mag órajel frekvenciája lehet. Az STM mikrovezérlő ezen modellje 168 MHz -es magórajelet biztosít. Bár ezzel a problémával foglalkozott ebben a projektben, általános elképzelés van erről a modellről, hogy nem pontosan ilyen magas frekvenciát biztosít.
A nyílt hurok sebessége nagyon sima vonalat biztosít, csak néhány váratlan értékkel. A PID algoritmus működőképes, és nagyon alacsony beállási időt biztosít a motornak. A motor PID algoritmusát különböző feszültségek mellett tesztelték, a referenciasebességet állandó értéken tartva. A feszültségváltozás nem változtatja meg a motor fordulatszámát, ami azt mutatja, hogy a PID algoritmus működik
Hatékonyság
Itt tárgyaljuk a PID szabályozó hatékonyságát, amelyet a kísérlet során figyeltünk meg.
Egyszerű megvalósítás
A kísérletek és megfigyelések részben láttuk, hogy a PID szabályozó nagyon könnyen megvalósítható. Csak három paramétert vagy állandót kell megadni ahhoz, hogy sebességszabályozó rendszer legyen
Páratlan hatékonyság a lineáris rendszerekhez
A lineáris PID szabályozó a leghatékonyabb a vezérlőcsaládban, mivel a logika nagyon egyszerű, és az alkalmazás széles körben elterjedt lineáris vagy meglehetősen lineáris alkalmazások esetén.
Korlátozások
Elvontan kifejtettük a rendszer korlátait. Itt megvitatunk néhányat, amelyeket megfigyeltünk.
Állandók kiválasztása
Láttuk, hogy bár a PID -szabályozó könnyen megvalósítható, a rendszer nagy hátránya, hogy az állandók értékének kiválasztása fáradságos; mivel nehéz számításokat kell végezni. A másik módszer a találat és próba módszer, de ez sem hatékony.
Az állandó nem mindig állandó
A kísérleti eredmények azt mutatták, hogy a motor referencia fordulatszámának különböző értékei esetén a PID szabályozó hibásan működött a PID állandók azonos értékei esetén. Különböző sebességek esetén az állandókat különböző módon kellett kiválasztani, és ez exponenciálisan növeli a számítási költségeket.
Nem lineáris
A mi esetünkben használt PID szabályozó lineáris, ezért csak lineáris rendszerekre alkalmazható. Nemlineáris rendszerek esetén a vezérlőt különböző módon kell megvalósítani. Bár rendelkezésre állnak különböző nemlineáris PID módszerek, ezek több paramétert igényelnek. Ez ismét nem kívánatosvá teszi a rendszert a magas számítási költségek miatt.
Kezdeti push szükséges
A kísérleti részben megmutattuk, hogy meglehetősen kis referenciasebességnél, ahol a hiba meglehetősen kicsi az induláskor, a PID által szolgáltatott PWM olyan kicsi, hogy nem hozza létre a szükséges indítónyomatékot a motor számára. Tehát a motor egyes kísérletekben nem jár, vagy más kísérletekben nagy túllépést és hosszabb ülepedési időt biztosít.
9. lépés: Külön köszönet
Külön köszönet a csoporttagjaimnak, akik segítettek nekem ebben a projektben.
Hamarosan feltöltöm a videó linkjét.
Remélem, érdekesnek találja ezt a tanulságosat.
Ez Tahir Ul Haq az UET -ből. Egészségére !!!
Ajánlott:
Önkiegyenlítő robot - PID vezérlő algoritmus: 3 lépés

Önkiegyenlítő robot - PID vezérlő algoritmus: Ez a projekt azért jött létre, mert többet akartam megtudni a vezérlőalgoritmusokról és a funkcionális PID hurkok hatékony megvalósításáról. A projekt még fejlesztési fázisban van, mivel még nincs hozzá Bluetooth modul, amely
Kordikus algoritmus a VHDL használatával: 4 lépés
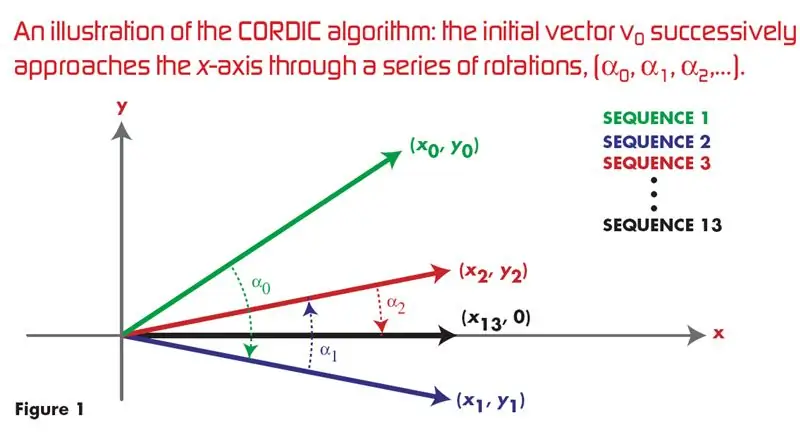
Kordikus algoritmus a VHDL használatával: ## Ez a leggyakrabban kattintott, legnépszerűbb link a Google -ban a CORDIC ALGORITHM VHDL megvalósításához, szinusz- és koszinuszhullám generálásához ## Jelenleg számos hardverhatékony algoritmus létezik, de ezek nem ismertek a a softwar dominanciája
Hogyan hozzunk létre egy távvezérelt 3D nyomtatott önegyensúlyozó robotot: 9 lépés (képekkel)

Hogyan hozzunk létre egy távirányítású 3D nyomtatott önegyensúlyozó robotot: Ez a B-robot korábbi verziójának továbbfejlesztése. 100% NYITOTT FORRÁS / Arduino robot. A CODE, a 3D alkatrészek és az elektronika nyitva vannak, így bátran módosítsa vagy készítse el a robot hatalmas verzióját. Ha kétségei, ötletei vannak, vagy segítségre van szüksége, forduljon
Önegyensúlyozó Robo-lovag: 7 lépés (képekkel)

Önegyensúlyozó Robo-lovag: A videojátékok és a társasjátékok nagyszerű módja annak, hogy időt töltsön barátaival és családjával. Néha úgy érzi, hogy offline időt szeretne tölteni, és elrakja az összes elektronikáját, máskor pedig a sport, az árkád vagy a harci játék virtuális világába merül
Az egyenáramú motor fordulatszámának szabályozása PID algoritmus használatával (STM32F4): 8 lépés (képekkel)

Az egyenáramú motor fordulatszámának szabályozása PID algoritmus (STM32F4) használatával: hello mindenkinek! Ez egy másik projekt. Ezúttal az STM32F407 az MC. Ez a félév végi projekt. Remélem, tetszik. Sok koncepciót és elméletet igényel, ezért először foglalkozunk vele. A számítógépek és a
