Társasjáték Mesterséges intelligencia: a Minimax algoritmus: 8 lépés

2024 Szerző: John Day | [email protected]. Utoljára módosítva: 2024-01-30 09:41

Gondolkozott már azon, hogyan készülnek azok a számítógépek, amelyek ellen sakkban vagy dáma ellen játszik? Nos, ne keressen tovább, mint ez az Instructable, mert megmutatja, hogyan lehet egyszerű, de hatékony mesterséges intelligenciát (AI) létrehozni a Minimax algoritmus használatával! A Minimax algoritmus használatával az AI jól megtervezett és átgondolt lépéseket hajt végre (vagy legalábbis utánoz egy gondolatmenetet). Most csak megadhatnám az általam készített AI kódját, de ez nem lenne szórakoztató. Elmagyarázom a számítógép választásának logikáját.

Ebben az utasításban bemutatom az Othello (AKA Reversi) mesterséges mesterséges intelligencia létrehozásának lépéseit a pythonban. A projekt kezelése előtt közbenső szinten meg kell értenie, hogyan kell kódolni a pythonban. Íme néhány jó webhely, amelyet meg kell néznie, hogy felkészüljön erre az utasításra: w3schools vagy learnpython. Ennek az utasításnak a végén rendelkeznie kell egy mesterséges intelligenciával, amely kiszámított lépéseket tesz, és képes lesz legyőzni a legtöbb embert.

Mivel ez az Instructable elsősorban az AI készítésével fog foglalkozni, nem fogom elmagyarázni, hogyan kell játékot tervezni pythonban. Ehelyett megadom annak a játéknak a kódját, ahol egy ember játszhat egy másik ember ellen, és úgy módosíthatom, hogy olyan játékot játszhasson, ahol az ember az AI ellen játszik.

A Columbia SHAPE nyári programján keresztül megtanultam, hogyan kell létrehozni ezt az AI -t. Jól éreztem magam ott, nézd meg a honlapjukat, hátha érdekel.

Most, hogy kizártuk a logisztikát, kezdjük el a kódolást!

(A képekhez tettem néhány megjegyzést, ezért feltétlenül nézze meg őket)

Kellékek

Ez könnyű:

1) Python környezetű számítógép, például Spyder vagy IDLE

2) Töltse le az Othello játék fájljait a GitHub -ból

3) Az agyad türelemmel telepítve

Lépés: Töltse le a szükséges fájlokat

Amikor belép a GitHub -ba, 5 fájlt kell látnia. Töltse le mind az 5 -öt, és helyezze őket ugyanabba a mappába. Mielőtt futtatnánk a játékot, nyissuk meg az összes fájlt a spyder környezetben.

Íme, mit csinálnak a fájlok:

1) az othello_gui.py ez a fájl létrehozza a játéktáblát, amin a játékosok játszhatnak (akár emberi, akár számítógépes)

2) az othello_game.py ez a fájl két számítógépet játszik egymás ellen a játéktábla nélkül, és csak a pontszámot és a mozgó pozíciókat mutatja

3) ai_template.py itt fogod elhelyezni az összes kódodat az AI készítéséhez

4) randy_ai.py ez egy előre elkészített AI, amely véletlenszerűen választja a lépéseit

5) othello_shared.py egy csomó előre elkészített funkció, amelyekkel mesterséges intelligenciáját készítheti, például a rendelkezésre álló lépések, pontszámok vagy táblaállapot ellenőrzésére

6) A három másik fájl: a Puma.py, az erika_5.py és a nathan.py, amelyeket én, Erika és Nathan készítettem a SHAPE programból, ez három különböző AI egyedi kóddal

2. lépés: A Python Othello megnyitása és lejátszása

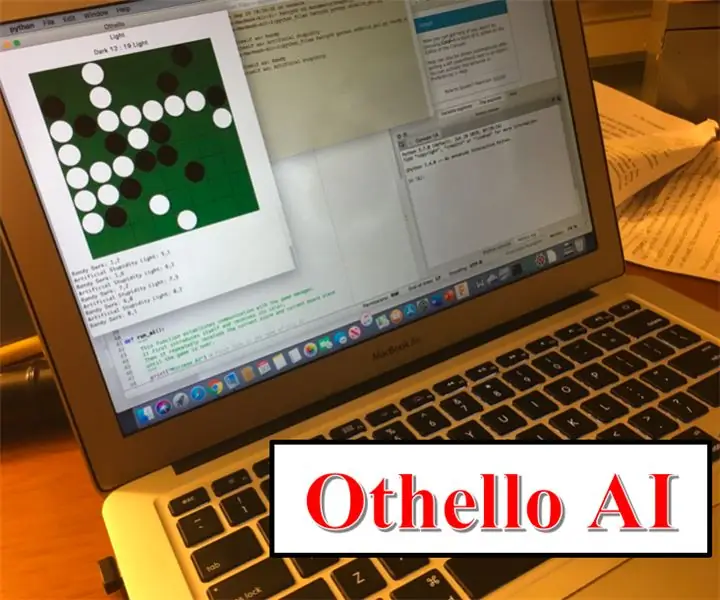
Miután megnyitotta az összes fájlt, írja be a képernyő jobb alsó sarkába a "run othello_gui.py" parancsot, és nyomja meg az Enter billentyűt az IPython konzolban. Vagy a Mac terminálban írja be a "python othello_gui.py" parancsot (miután természetesen a megfelelő mappába került). Ezután megjelenik egy tábla a képernyőn. Ez a mód az ember vs ember mód. A fény másodszor, a sötét először. Nézd meg a videómat, ha zavarban vagy. iA tetején az egyes színlapok pontszáma látható. A játékhoz kattintson egy érvényes mozgatási mezőre, és helyezzen egy lapkát oda, majd adja át a számítógépet ellenfelének, aki ugyanezt fogja tenni és megismétli.

Ha nem tudja, hogyan kell játszani az Othellóval, olvassa el ezeket a szabályokat az ultra táblák webhelyéről:

A fekete mindig először mozog. A lépést úgy hajtjuk végre, hogy a játékos színű korongját a táblára helyezzük olyan helyzetbe, amely "kívül áll" az ellenfél egy vagy több korongjával. A tárcsa vagy korongsor szegélyezett, ha a végén ellentétes színű lemezek veszik körül. Egy lemez tetszőleges számú lemezt szegélyezhet egy vagy több sorban bármilyen irányban (vízszintes, függőleges, átlós)…. (fejezze be az olvasást a weboldalukon)

A különbség az eredeti játék és ez a python játék között az, hogy amikor egyetlen játékosnak nincs érvényes mozdulata, a játék véget ér

Most, hogy játszhat a játékkal egy barátjával, készítsünk egy AI -t, amellyel játszhat.

3. lépés: Minimax algoritmus: forgatókönyvek létrehozása

Mielőtt arról beszélnénk, hogyan kell ezt kódba írni, nézzük át a mögöttes logikát. A minimumx algoritmus egy döntéshozó, visszamenőleges algoritmus, és általában kétjátékos, körökön alapuló játékokban használatos. Ennek az AI -nak az a célja, hogy megtalálja a következő legjobb lépést és a következő legjobb lépéseket, amíg meg nem nyeri a játékot.

Most hogyan határozná meg az algoritmus, hogy melyik lépés a legjobb? Álljon meg, és gondolja át, hogyan választaná a következő lépést. A legtöbb ember azt a lépést választaná, amely a legtöbb pontot adná nekik, igaz? Vagy ha előre gondolkodnak, akkor azt a lépést választják, amely olyan helyzetet teremt, amelyben még több pontot szerezhetnek. Az utóbbi gondolkodásmód a Minimax algoritmus gondolkodási módja. Előre tekint a tábla minden jövőbeni beállításánál, és megteszi azt a lépést, amely a legtöbb ponthoz vezetne.

Ezt visszalépési algoritmusnak neveztem, mert először azzal kezdődik, hogy először létrehozza és értékeli az összes jövőbeni táblaállapotot a hozzájuk tartozó értékekkel. Ez azt jelenti, hogy az algoritmus annyian játssza a játékot, amennyire szüksége van (a mozdulatokat magának és az ellenfélnek), amíg a játék minden forgatókönyve el nem játszódik. Az összes táblaállapot (forgatókönyv) nyomon követéséhez rajzolhatunk egy fát (nézze meg a képeket). A fenti képen látható fa egy egyszerű példa a Connect 4 játékra. Minden táblakonfigurációt táblaállapotnak neveznek, és a fán elfoglalt helyét csomópontnak. A fa alján lévő összes csomópont a végső táblaállapot az összes lépés végrehajtása után. Nyilvánvaló, hogy egyes táblaállapotok jobbak az egyik játékos számára, mint a másik. Tehát most ki kell választanunk az AI -t, hogy melyik táblaállapothoz kíván eljutni.

4. lépés: Minimax: A tábla konfigurációinak értékelése

Ahhoz, hogy értékeket adjunk a táblaállapotoknak, meg kell tanulnunk az általunk játszott játék stratégiáit: ebben az esetben Othello stratégiáit. Mivel ez a játék az ellenfél és a korongok felforgatásának harca, a legjobb korongpozíciók azok, amelyek stabilak és nem fordíthatók meg. A sarok például az a hely, ahol a lemez behelyezésekor nem lehet másik színre váltani. Így ez a hely rendkívül értékes lenne. További jó pozíciók közé tartoznak a tábla oldalai, amelyek lehetővé teszik, hogy sok követ vegyen. Ezen a webhelyen több stratégia található.

Most értékeket rendelhetünk az egyes táblaállapot -táblák pozícióihoz. Ha egy pozíciót elfoglal az AI darabja, akkor a pozíciótól függően bizonyos számú pontot ad. Például egy táblaállapotban, ahol az AI darabja a sarokban van, 50 pont bónuszt adhat, de ha kedvezőtlen helyen lenne, a darab értéke 0 lehet. Miután figyelembe vette a a pozíciókat, értéket rendel a tábla állapotához. Például, ha az AI -nak van egy darabja a sarokban, akkor a tábla állapota 50, míg egy másik táblaállapot, amelynek közepén az AI darabja, 10.

Ennek számos módja van, és három különböző heurisztikám van a tábladarabok értékeléséhez. Azt javaslom, hogy készítsen saját típusú heurisztikát. Három különböző mesterséges intelligenciát töltöttem fel a githubomba, három különböző gyártó által, három különböző heurisztikával: Puma.py, erika5.py, nathanh.py.

5. lépés: Minimax algoritmus: A legjobb lépés kiválasztása

Most jó lenne, ha az AI csak választhatna minden lépést, hogy a legmagasabb pontszámmal juthasson el a tábla állapotába. De ne feledje, hogy az AI is választotta a lépéseket az ellenfél számára, amikor az összes táblaállapotot generálta, és ha az ellenfél okos, akkor nem teszi lehetővé, hogy az AI elérje a legmagasabb táblás pontszámot. Ehelyett egy okos ellenfél megtenné a lépést, hogy az AI a legalacsonyabb táblás állapotba kerüljön. Az algoritmus szerint a két játékost maximalizáló játékosnak és minimalizáló játékosnak nevezzük. Az AI lenne a maximalizáló játékos, mivel a legtöbb pontot akarja megszerezni magának. Az ellenfél lenne a minimalizáló játékos, mivel az ellenfél megpróbálja megtenni azt a lépést, ahol az AI kapja a legkevesebb pontot.

Miután az összes táblaállapot létrejött, és az értékek hozzá lettek rendelve a táblákhoz, az algoritmus elkezdi összehasonlítani a táblaállapotokat. A képeken létrehoztam egy fát, amely bemutatja, hogyan választja meg az algoritmus a lépéseit. Az ágak minden osztása más lépés, amelyet az AI vagy az ellenfél játszhat. A csomópontok soraitól balra írtam, hogy a maximalizáló vagy a minimalizáló játékos megy -e. Az alsó sorban a tábla összes állapota látható értékekkel. Mindegyik csomópont belsejében van egy szám, és ezek a pontszámok, amelyeket az egyes táblákhoz rendelünk: minél magasabbak, annál jobb az AI.

Definíciók: szülőcsomópont - csomópont, amely csomópontokat eredményez vagy hoz létre alatta; a gyermekcsomópontok eredete - azok a csomópontok, amelyek ugyanabból a szülőcsomópontból származnak

Az üres csomópontok azt jelzik, hogy az AI melyik mozgatásával jut el a legjobb táblaállapothoz. A bal oldali csomópont gyermekeinek összehasonlításával kezdődik: 10, -3, 5. Mivel a maximalizáló játékos hajtja végre a lépést, azt a lépést választja, amely a legtöbb pontot adja: 10. Tehát kiválasztjuk és eltároljuk lépjen a tábla pontszámával, és írja be a szülőcsomópontba. Most, hogy a 10 a szülőcsomópontban van, most a minimalizáló játékosokon van a sor. A csomópont azonban, amelyhez 10 -et hasonlítunk, üres, ezért először ki kell értékelnünk azt a csomópontot, mielőtt a minimalizáló játékos választhat. Tehát visszatérünk a maximalizáló játékos köréhez, és összehasonlítjuk a szomszédos csomópont gyermekeit: 8, -2. A maximalizálás 8 -at választ, és ezt írjuk az üres szülőcsomópontba. Most, hogy az algoritmus befejezte az üres helyek kitöltését a felette lévő csomópont gyermekei számára, a minimalizáló játékos összehasonlíthatja ezeket a gyerekeket - 10 és 8, és választhat a 8. Az algoritmus ezt követően megismétli ezt a folyamatot, amíg a teljes fa ki nem töltődik. Ennek a példának a végén a 8. pontszámunk van. Ez a legmagasabb táblaállapot, amit az AI játszhat, ha feltételezi, hogy az ellenfél optimálisan játszik. Tehát az AI választja az első lépést, amely a 8 táblás állapotba vezet, és ha az ellenfél optimálisan játszik, akkor az AI -nak minden lépést el kell végeznie, hogy a 8. táblás állapotba kerüljön. (Kövesse a képeken található megjegyzéseket)

Tudom, hogy ez sok volt. Ha Ön egyike azoknak a típusoknak, akiknek beszélniük kell veled, hogy valamit megértsenek, itt van néhány videó, amelyeket megnéztem, hogy segítsek megérteni a mögöttes ötletet: 1, 2, 3.

6. lépés: Minimax algoritmus: pszeudokód

Miután megértette a minimumx algoritmus mögötti logikát, nézze meg ezt az álkódot (az összes kódra univerzális funkciókat) a wikipédiából:

függvény minimumx (csomópont, mélység, maximalizáló játékos) az

ha a mélység = 0 vagy a csomópont egy terminális csomópont, akkor

visszaadja a csomópont heurisztikus értékét

ha maximalizálja a lejátszót akkor

érték: = −∞

csomópont minden gyermeke esetén

érték: = max (érték, minimumx (gyermek, mélység - 1, HAMIS))

visszatérési érték

else (* játékos minimalizálása *)

érték: = +∞

csomópont minden gyermeke esetén

érték: = min (érték, minimumx (gyermek, mélység - 1, IGAZ))

visszatérési érték

Ez egy rekurzív függvény, vagyis újra és újra hívja magát, amíg el nem éri a leállási pontot. Először is, a függvény három értéket vesz fel, a csomópontot, a mélységet és azt, hogy kié a sor. A csomópont értéke az a hely, ahol a program elkezdi keresni. A mélység az, hogy milyen messzire szeretné a program keresni. Például a fa példámban 3 mélységű, mert 3 lépés után átkutatta az összes táblaállapotot. Természetesen szeretnénk, ha az AI minden táblaállapotot ellenőrizne, és győztes győzelmet választana, de a legtöbb játékban, ahol több ezer, ha nem több millió táblakonfiguráció létezik, az otthoni laptop nem tudja feldolgozni ezeket a konfigurációkat. Tehát korlátozzuk az AI keresési mélységét, és a legjobb tábla állapotba kerülünk.

Ez az álkód az előző két lépésben kifejtett folyamatot reprodukálja. Most tegyünk egy lépést tovább és javítsuk ezt a python kódban.

7. lépés: AI készítése az Ai_template.py segítségével

Mielőtt megnézné a Minimax AI kódomat, tegyen egy próbát arra, hogy saját AI-t készítsen az ai_template.py fájllal és az álkóddal, amelyről az utolsó lépésben beszéltünk. Az ai sablonnak két funkciója van: def minimumx_min_node (tábla, szín) és def minimumx_max_node (tábla, szín). Ahelyett, hogy a minimumx függvény rekurzívan hívná magát, két különböző függvényünk van, amelyek egymást hívják. A heurisztika létrehozásához az alaplapok állapotának értékeléséhez létre kell hoznia saját funkcióját. Van egy előre elkészített funkció az othello_shared.py fájlban, amelyet felhasználhat AI létrehozásához.

Ha megvan az AI, próbálja meg futtatni a randy_ai.py ellen. Két ais egymás elleni futtatásához írja be a "python othello_gui.py (illessze be az ai fájlnevet).py (illessze be a fájl nevét).py" címet a Mac terminálba, vagy írja be a "run othello_gui.py (ai fájlnév beillesztése).py (illessze be a fájlnevet).py ", és győződjön meg arról, hogy a megfelelő könyvtárban van. Ezenkívül nézze meg a videómat a pontos lépésekért.

8. lépés: Ideje harcolni az AI -val

Most szerezzen be egy csomó számítógépes barátot, és tervezze meg saját mesterséges intelligenciáját! Akkor versenyt írhatsz, és kiveheted az AI -dukádat. Remélhetőleg, még ha nem is tudná felépíteni saját mesterséges intelligenciáját, megértené, hogyan működik a minimumx algoritmus. Ha bármilyen kérdése van, tegye fel kérdéseit az alábbi megjegyzésekben.